2. Локальные, глобальные и специальные группы. Локальная группа это группа
локальная группа - это... Что такое локальная группа?
Большой англо-русский и русско-английский словарь. 2001.
- локальная гомология
- локальная группа данных
Смотреть что такое "локальная группа" в других словарях:
локальная группа — vietinė grupė statusas T sritis fizika atitikmenys: angl. local group vok. lokale Gruppe, f rus. локальная группа, f pranc. groupe local, m … Fizikos terminų žodynas
ЛОКАЛЬНАЯ ГРУППА ГАЛАКТИК — ЛОКАЛЬНАЯ ГРУППА ГАЛАКТИК, небольшая группа примерно из 30 ГАЛАКТИК, куда входит и наша Галактика, два Магеллановых Облака, Туманность Андромеды и спиральная галактика в созвездии Треугольника. Неравномерно распределены по эллипсовидному… … Научно-технический энциклопедический словарь
локальная группа пользователей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN local user groupLUG … Справочник технического переводчика
ЛИ ЛОКАЛЬНАЯ ГРУППА — аналитическая локальная группа, аналитическое многообразие Gнад полем k, полным относительно нек рого нетривиального абсолютного значения, снабженное отмеченным элементом е(единицей), открытым подмножеством и парой аналитич. отображений… … Математическая энциклопедия
Локальная топологическая группа — Локальная топологическая группа топологическая группа, в которой групповые операции определены лишь для элементов, достаточно близких к единице. Введение локальных топологических групп было инспирировано изучением локальной структуры… … Википедия
Локальная популяция — * лакальная папуляцыя * local polulation группа особей одного вида, проживающая на территории, в пределах которой они в основном спариваются между собой. Сином термина «локальная популяция» являются также термины «дим» и «менделевская популяция» … Генетика. Энциклопедический словарь
ГРУППА СУСЛОВИЕМ КОНЕЧНОСТИ — группа, элементы или подгруппы к рой удовлетворяют тому или иному условию конечности. Под условием конечности в теории групп понимается любое такое свойство, присущее всем конечным группам, что существуют бесконечные группы, к рые им не обладают … Математическая энциклопедия
Локальная теорема — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
ГРУППА — один из основных типов алгебраических систем. Теория Г. изучает в самой общей форме свойства алгебраич. операций, наиболее часто встречающихся в математике и ее приложениях (примеры таких операций умножение чисел, сложение векторов,… … Математическая энциклопедия
ГРУППА С ОДНОЗНАЧНЫМ ИЗВЛЕЧЕНИЕМ КОРНЯ — R группа группа, у к рой из равенства следует , где х, у любые элементы группы, п любое натуральное число. Группа Gтогда и только тогда является R группой, когда она без кручения и такова, что нз следует для любых п натурального числа п. R группа … Математическая энциклопедия
ЛОКАЛЬНАЯ ТОПОЛОГИЧЕСКАЯ ГРУППА — топологическая группа, в к рой групповые операции определены лишь для элементов, достаточно близких к единице. Введение Л. т. г. было инспирировано изучением локальной структуры топологич. групп (т. е. их структуры в сколь угодно малой… … Математическая энциклопедия
dic.academic.ru
локальная группа - это... Что такое локальная группа?
локальная группаУниверсальный русско-английский словарь. Академик.ру. 2011.
- локальная граница роуминга
- локальная группа данных
Смотреть что такое "локальная группа" в других словарях:
локальная группа — vietinė grupė statusas T sritis fizika atitikmenys: angl. local group vok. lokale Gruppe, f rus. локальная группа, f pranc. groupe local, m … Fizikos terminų žodynas
ЛОКАЛЬНАЯ ГРУППА ГАЛАКТИК — ЛОКАЛЬНАЯ ГРУППА ГАЛАКТИК, небольшая группа примерно из 30 ГАЛАКТИК, куда входит и наша Галактика, два Магеллановых Облака, Туманность Андромеды и спиральная галактика в созвездии Треугольника. Неравномерно распределены по эллипсовидному… … Научно-технический энциклопедический словарь
локальная группа пользователей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN local user groupLUG … Справочник технического переводчика
ЛИ ЛОКАЛЬНАЯ ГРУППА — аналитическая локальная группа, аналитическое многообразие Gнад полем k, полным относительно нек рого нетривиального абсолютного значения, снабженное отмеченным элементом е(единицей), открытым подмножеством и парой аналитич. отображений… … Математическая энциклопедия
Локальная топологическая группа — Локальная топологическая группа топологическая группа, в которой групповые операции определены лишь для элементов, достаточно близких к единице. Введение локальных топологических групп было инспирировано изучением локальной структуры… … Википедия
Локальная популяция — * лакальная папуляцыя * local polulation группа особей одного вида, проживающая на территории, в пределах которой они в основном спариваются между собой. Сином термина «локальная популяция» являются также термины «дим» и «менделевская популяция» … Генетика. Энциклопедический словарь
ГРУППА СУСЛОВИЕМ КОНЕЧНОСТИ — группа, элементы или подгруппы к рой удовлетворяют тому или иному условию конечности. Под условием конечности в теории групп понимается любое такое свойство, присущее всем конечным группам, что существуют бесконечные группы, к рые им не обладают … Математическая энциклопедия
Локальная теорема — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
ГРУППА — один из основных типов алгебраических систем. Теория Г. изучает в самой общей форме свойства алгебраич. операций, наиболее часто встречающихся в математике и ее приложениях (примеры таких операций умножение чисел, сложение векторов,… … Математическая энциклопедия
ГРУППА С ОДНОЗНАЧНЫМ ИЗВЛЕЧЕНИЕМ КОРНЯ — R группа группа, у к рой из равенства следует , где х, у любые элементы группы, п любое натуральное число. Группа Gтогда и только тогда является R группой, когда она без кручения и такова, что нз следует для любых п натурального числа п. R группа … Математическая энциклопедия
ЛОКАЛЬНАЯ ТОПОЛОГИЧЕСКАЯ ГРУППА — топологическая группа, в к рой групповые операции определены лишь для элементов, достаточно близких к единице. Введение Л. т. г. было инспирировано изучением локальной структуры топологич. групп (т. е. их структуры в сколь угодно малой… … Математическая энциклопедия
universal_ru_en.academic.ru
Изучите состав и назначение встроенных рабочих групп. — МегаЛекции
В Windows ХР Professional предусмотрено две категории встроенных групп, локальные и системные, позволяющие упростить назначение прав и разрешений для часто выполняемых задач.
Группа (group) — это совокупность учетных записей пользователей. Группы упрощают администрирование, позволяя назначить разрешения и права для группы пользователей, а не индивидуально для каждой учетной записи (рис. 9).
Рис. 9. Группы упрощают администрирование
Посредством разрешений (permissions) можно определить права пользователей при работе с ресурсами типа папки, файла или принтера. Назначив разрешения, вы предоставляете пользователям доступ к ресурсу и определяете тип доступа, который они имеют. Например, если нескольким пользователям необходимо прочесть некий файл, то можно объединить их учетные записи в группу и затем предоставить этой группе разрешение на чтение этого файла. Права (rights) позволяют пользователям выполнять системные задачи, например изменять время, выполнять архивацию и восстановление файлов.
Локальные группы
Локальная группа (local group) — совокупность учетных записей пользователей на компьютере. Локальные группы используются при назначении разрешений на доступ к ресурсам, постоянно хранящимся на компьютере, где создана локальная группа. Windows ХР Professional создает локальные группы в базе данных локальных политик безопасности.
Подготовка к применению локальных групп
• Используйте локальные группы на компьютерах, которые не входят в домен.
Вы можете использовать локальные группы только на компьютере, где они создаются. Хотя локальные группы доступны на рядовых серверах и компьютерах домена на платформе Windows 2000 Server, не используйте локальные группы на компьютерах, которые являются частью домена. Применение локальных групп на компьютерах домена лишает вас возможности централизованного администрирования группы. Локальные группы недоступны в каталоге Active Directory, и вам придется управлять ими отдельно ни каждом компьютере.
• Разрешения локальных групп предоставляют доступ к ресурсам только на компьютере, где вы их создаете.
Примечание Нельзя создать локальные группы на контроллерах домена, потому что контроллеры домена не могут иметь независимой от Active Directory базы данных политик безопасности.
Правила членства в локальных группах включают следующее:
• локальные группы могут объединять только локальные учетные записи пользователей системы, где эти группы создаются;
• локальные группы не могут принадлежать никакой другой группе.
Удаление локальных групп
Для удаления локальных групп используйте оснастку Управление компьютером (Computer Management). Каждая создаваемая вами группа имеет уникальный идентификатор, который никогда повторно не используется. Windows XP Professional применяет его для идентификации группы и ее разрешений. При удалении группы Windows XP professional снова этот идентификатор не использует, даже если вы создаете новую группу с таким же, как у удаленной группы, именем. Поэтому не удастся восстановить доступ к ресурсам, повторно создав группу.
При удалении группы вы удаляете только группу и ее разрешения и права. При этом не удаляются учетные записи пользователей, которые являются членами группы. Чтобы удалить группу, щелкните правой кнопкой мыши имя группы в оснастке Управление компьютером, затем щелкните пункт меню Удалить.
Встроенные локальные группы
Все изолированные серверы, рядовые серверы и компьютеры на платформе Windows XP Professional имеют встроенные локальные группы (built-in local groups). Они дают право выполнять системные задачи на отдельно взятом компьютере — резервное копирование и восстановление файлов, изменение времени и управление системными ресурсами. Windows XP Professional хранит встроенные локальные группы в папке Группы (Groups) оснастки Управление компьютером.
В таблице 2.2 перечислены встроенные локальные группы и описаны их возможности. За исключением отдельно оговоренных случаев, эти группы не имеют исходных членов.
Встроенные системные группы
Встроенные системные группы существуют на всех компьютерах под управлением Windows XP Professional. Системные группы не имеют определенных членств, которые можно изменять, но в них входят различные пользователи в разное время, в зависимости от того, каким образом пользователь получает доступ к системе или ресурсам. Системные группы не видны, когда Вы администрируете группы, но они доступны при назначении прав и разрешений для ресурсов. Windows XP Professional организует членство в системных группах в зависимости от вида доступа к компьютеру, а не от личности пользователя. В таблице 2.3 перечислены встроенные системные группы и описаны их возможности.
Возможности встроенной локальной группы Таблица 2.2
| Локальная группа | Описание |
| Администраторы (Administrators) | Члены этой группы могут выполнять все административные задачи на компьютере. По умолчанию встроенная учетная запись администратора является членом этой группы. Когда к домену подключается рядовой сервер или компьютер на платформе Windows XP Professional, Windows 2000 Server добавляет группу Domain Admins (Администраторы домена) в локальную группу администраторов |
| Операторы архива(Backup Operators) | Члены этой группы могут выполнять резервное копирование и восстановление системных компонентов с помощью служебной программы Архивация Windows (Windows Backup) |
| Гости (Guests) | Члены этой группы могут: • выполнять только задачи, для которых им предоставлены права; • пользоваться только теми ресурсами, на доступ к которым они имеют разрешения. Члены этой группы не могут производить постоянные изменения конфигурации рабочего стола. По умолчанию встроенная гостевая учетная запись является членом этой группы. Когда рядовой сервер или компьютер на платформе Windows XP Professional присоединяется к домену, Windows 2000 Server добавляет группу Domain Guests (Гости домена) в локальную группу Гости (Guests) |
| Опытные пользователи (Power Users) | Члены этой группы могут создавать и изменять локальные учетные записи пользователей на компьютере и совместно использовать ресурсы |
| Репликатор (Replicator) | Занимается дублированием файлов в домене |
| Пользователи (Users) | Члены этой группы могут: • выполнять только задачи, для которых им были предоставлены права; • пользоваться только теми ресурсами, для которых они имеют разрешения. По умолчанию Windows XP Professional добавляет в группу Пользователи (Users) все локальные учетные записи пользователей, которые администратор создает на компьютере. Когда рядовой сервер или компьютер на платформе Windows XP Professional присоединяется к домену, Windows 2000 Server добавляет группу Domain Users (Пользователи домена) в локальную группу Пользователи (Users) |
Возможности встроенных системных групп Таблица 2.3
| Системная группа | Описание |
| Все (Everyone) | Все пользователи, которые имеют доступ к компьютеру. По умолчанию при форматировании тома в NTFS, группе Все (Everyone) предоставляется разрешение полного доступа. Это вызывало проблемы в более ранних версиях Windows, в том числе и Microsoft Windows 2000. В Windows XP Professional анонимный вход в систему теперь не включен в группу Все (Everyone). При переходе с Windows 2000 Professional на Windows XP Professional ресурсы с разрешениями для группы Все (Everyone), а не специально для группы анонимного входа в систему, недоступны группе анонимного входа в систему |
| Прошедшие проверку (Authenticated Users) | Все пользователи с действительными учетными записями пользователя на компьютере. (Если ваш компьютер — часть домена, все пользователи включаются в Active Directory) |
| Создатель-владелец (Creator Owner) | Эта учетная запись пользователя для тех, кто создал или владеет ресурсом. Если ресурс создает член группы администраторов, то ресурсом владеет группа администраторов. |
| Сеть (Network) | Любой пользователь с удаленным подключением к общему ресурсу на этом компьютере. |
| Интерактивные (Interactive) | Учетная запись для пользователя, вошедшего в систему. Члены интерактивной группы могут пользоваться физическими ресурсами системы. При входе в систему они получают доступ к ресурсам компьютера «интерактивно» |
| Анонимный вход (Anonymous Logon) | Любая учетная запись, подлинность которой Windows XP Professional подтвердить не может |
| Удаленный доступ (Dialup) | Любой пользователь, кто в настоящее время имеет удаленный доступ к компьютеру через модем |
ВОПРОСЫ К ДОМАШНИМ ЗАДАНИЯМ
1. Что представляет собой Рабочая группа Windows XP Professional?
2. В каких случаях применение рабочей группы нецелесообразно?
3. Что такое контроллер домена?
4. Какие действия можно произвести с учетной записью гостя?
5. Каково максимальное количество символов, которое Windows XP Professional признает в имени локальной учетной записи пользователя?
6. Если пользователи создают свои собственные пароли, каких рекомендаций они должны придерживаться?
7. Для чего предназначена категория Учетные записи пользователей (User Accounts)?
8. Какие свойства локальной учетной записи пользователя?
9. Для чего применяется профиль пользователя?
10. Что такое Локальные группы и зачем они нужны?
11. Можно ли управлять Локальными группами централизованно?
12. Что такое профили пользователей и зачем они нужны?
13. Можно ли восстановить доступ к ресурсам, заново создав группу?
14. При удалении группы удаляются ли ее разрешения и права?
15. При удалении группы удаляются ли учетные записи пользователей, которые являются членами этой группы?
16. Какая разница между встроенными системными группами и встроенными локальными группами в системах под управлением Windows XP Professional? Приведите хотя бы два примера каждого типа группы.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
ЛИ ЛОКАЛЬНАЯ ГРУППА - это... Что такое ЛИ ЛОКАЛЬНАЯ ГРУППА?
аналитическая локальная группа,- аналитическое многообразие Gнад полем k, полным относительно нек-рого нетривиального абсолютного значения, снабженное отмеченным элементом е(единицей), открытым подмножеством и парой аналитич. отображений многообразия окрестности Uв себя, для которых:
1) в некоторой окрестности точки евыполняется тождество ge=eg;
2) в некоторой окрестности точки евыполняется тождество
3,) для некоторой окрестности точки евыполняется включение причем g(hr)=(gh)r, где g, h, r - любые элементы из V.
Ли л. г. впервые появились в трудах С. Ли (S. Lie) и его школы (см. [1]) как локальные Ли, группы преобразований.
Пусть G1 и G2- две Ли л. г. с единицами е 1 н е 2 соответственно. Локальным гомоморфизмом G1 в G2 (обозначается ) наз. аналитич. отображение нек-рой окрестности в G1, для к-рого f(e1)=e2 и f(gh)=f(g)f(h).для g, h из нек-рой окрестности точки е 1. Определяемая естественным образом композиция локальных гомоморфизмов также есть локальный гомоморфизм. Локальные гомоморфизмы совпадающие в нек-рой окрестности точки е 1 наз. эквивалентными. Если существуют такие локальные гомоморфизмы и что композиции эквивалентны тождественным отображениям, то Ли л. г. G1 и G2 наз. эквивалентными.
Пример. Пусть - аналитич. руппа с единицей е к G - открытая окрестность точки ев Тогда аналитич. структура на индуцирует аналитич. структуру на G, причем операции умножения и взятия обратного элемента в превращают G в Ли л. г. (в частности, сама может рассматриваться как Ли л. г.). Все Ли л. г. G, получаемые таким способом из фиксированной аналитич. руппы эквивалентны между собой.
Один из принципиальных вопросов теории групп Ли состоит в том, насколько общий характер имеет приведенный выше пример, т. е. будет ли всякая Ли л. г. (с точностью до эквивалентности) окрестностью нек-рой аналитич. руппы. Ответ на этот вопрос положителен (см. [2], [3], [4]), в случае банаховых Ли л. г. ответ отрицателен (см. [4J).
Важнейшим средством изучения Ли л. е - ее единица. Выбор карты с аналитич. многообразия G в точке епозволяет отождествить нек-рую окрестность точки е в G с нек-рой окрестностью Uнуля в re-мерном координатном пространстве kn, так что Uстановится Ли л. г. Пусть U0 - такая окрестность нуля в Ли л. г. U, что для любых х,определено произведение Тогда в координатной форме умножение в Ли л. г. Uв окрестности U0 задается паналитич. функциями
где
- соответственно координаты точек В достаточно малой окрестности нуля функция fi представляется в виде суммы сходящегося степенного ряда (также обозначаемого далее через fi), а наличие в Uединицы и ассоциативного закона выражается следующими свойствами этих рядов, рассматриваемых как формальные степенные ряды от 2n переменных:
Свойства а) н о) означают, что система формальных степенных рядов является формальной группой. В частности, однородная компонента степени 2 каждого из рядов fi является билинейной формой на kn, т. е. имеет вид
что позволяет определить на kn умножение [ , ] по правилу:
Относительно этого умножения kn является алгеброй Ли. Указанная структура алгебры Ли переносится в касательное пространство к многообразию G в точке ес помощью определенного картой с изоморфизма Формальные группы Fc и Fc', определенные разными картами, изоморфны, а указанная структура алгебры Ли на не зависит от выбора карты с. Алгебра Ли наз. алгеброй Ли локальной группы Л и. Для любого локального гомоморфизма Ли л. г. его дифференциал в единице является гомоморфизмом алгебр Ли, откуда следует, что сопоставление Ли л. г. ее алгебры Ли является функториальным. В частности, эквивалентные Ли л. г. имеют изоморфные алгебры Ли.
Если поле kимеет характеристику 0, указанная выше конструкция, восходящая к С. Ли [1], позволяет свести изучение свойств Ли л. г. к изучению соответствующих свойств их алгебр Ли. В этом случае алгебра Ли g определяет Ли л. г. G однозначно с точностью до эквивалентности. А именно, карта сможет быть выбрана так, что произведение ху в Ли л. г. Uвыражается в виде нек-рого сходящегося ряда (т. н. ряда Кэмпбелла - Хаусдорфа) от элементов пространства kn, полученных из х к у с помощью операции коммутирования [ , ] и умножения на элементы из k(см. Кэмпбелла - Хаусдорфа формула). Обратно, для произвольной конечномерной алгебры Ли над kряд Кэмпбелла - Хаусдорфа сходится в нек-рой окрестности нуля в и определяет в этой окрестности структуру Ли л. г. с алгеброй Ли Таким образом, для любой заданной алгебры Ли существует единственная с точностью до эквивалентности Ли л. г., алгеброй Ли к-рой является Более того, всякий гомоморфизм алгебр Ли индуцирован нек-рым единственным гомоморфизмом соответствующих Ли л. г. Иначе говоря, сопоставление Ли л. г. ее алгебры Ли определяет эквивалентность категории Ли л. г. и категории конечномерных алгебр Ли над k. Кроме того, сопоставление Ли л. г. соответствующей формальной группы определяет эквивалентность категории Ли л. г. и категории формальных групп над k.
Алгебра Ли может быть определена и для любой банаховой Ли л. г.; основной результат об эквивалентности категорий Ли л. г. и алгебр Ли обобщается на этот случай (см. [2]).
Лит.:[1] L i e S., E n g е 1 P., Theorie der Transformationsgruppen, Bd 1-3, Lpz., 1888-93; [2] Б у р б а к и Н., Группы и алгебры Ли. Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с франц., М., 1976; [3] П о н т р я г и н Л. С., Непрерывные группы, 3 изд., М., 1973; [4] С е р р Ж.-П., Алгебры Ли и группы Ли, пер. с англ. и франц., М., 1969; [5] Чеботарев Н. Г., Теория групп Ли, М.- Л., 1940. В.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru
2. Локальные, глобальные и специальные группы
Windows NT Server использует три типа групп: локальные, глобальные и специальные. Каждый тип имеет свое назначение, возможности и ограничения.
Локальная группа может определяться для домена или для компьютера. Локальные группы дают пользователям права и разрешения на ресурсы того компьютера (или домена), где хранится учетная информация локальной группы. Доступ к ресурсам компьютера - Windows NT Workstation или Windows NT Server могут быть определены только для членов локальной группы этого компьютера, даже если эти компьютеры яваляются членами домена. Например, доступ к ресурсам сервера Windows NT Server 2 на рисунке 5.1 может быть определен только для пользователей, учетные данные которых хранятся в SAM 2 этого компьютера.
Так как база SAM PDC копируется на все BDC домена, то пользователи, определенные в PDC, могут иметь права на ресурсы как PDC, так и всех BDC домена.
Доступ к ресурсам компьютера для пользователей домена обеспечивается за счет механизма включения в локальную группу отдельных пользователей домена и глобальных групп домена. Включенные пользователи и группы получают те же права доступа, что и другие члены данной группы. Механизм включения глобальных групп в локальные является основным средством централизованного администрирования прав доступа в домене Windows NT.
Локальная группа не может содержать другие локальные группы. Поэтому в сети, использующей модель рабочей группы нет возможности определить на одном компьютере всех пользовавтелей сети и предоставлять им доступ к ресурсам других компьютеров.
В любом случае локальная группа объединяет некоторое число пользователей и глобальных групп, которым присваивается общее имя - имя локальной группы. Локальные группы могут включать пользователей и глобальные группы не только данного домена, но и любых доверяемых доменов.
Windows NT Workstation и Server поддерживают несколько встроенных локальных групп для выполнения системных задач. Администратор может создавать дополнительные локальные группы для управления доступом к ресурсам. Встроенные локальные группы делятся на две категории - администраторы (Administrators), которые имеют все права и разрешения на данный компьютер, и операторы, которые имеют ограниченные права на выполнение специфических задач. Для Windows NT Server имеются следующие группы-операторы: операторы архивирования (Backup Operator), репликаторы (Replicator), операторы сервера (Serevr Operator), принт-операторы (Print Operator) и операторы учетной информации (Account Operator). Для Windows NT Workstation имеется только две группы операторов - Backup Operators и Power Users.
Кроме того, как на Windows NT Server, так и на Windows NT Workstation имеются втроенные локальные группы Users - для обычных пользователей, и Guests - для временных пользователей, которые не могут иметь профиля и должны обладать минимальными правами.
Для упрощения организации предоставления доступа пользователям из другого домена в Windows NT введено понятие глобальной группы.
Глобальная группа пользователей - это группа, которая имеет имя и права, глобальные для всей сети, в отличие от локальных групп пользователей, которые имеют имена и права, действительные только в пределах одного домена. Администратор доверяющего домена может предоставлять доступ к ресурсам своего домена пользователям из глобальных групп тех доменов, которым данный домен доверяет. Глобальные группы можно включать в состав локальных групп пользователей ресурсного домена.
Глобальная группа - это некоторое число пользователей одного домена, которые группируются под одним именем. Глобальным группам могут даваться права и разрешения путем включения их в локальные группы, которые уже имеют требуемые права и разрешения. Глобальная группа может содержать только учетную информацию пользователей из локальных учетных баз данных, она не может содержать локальные группы или другие глобальные группы.
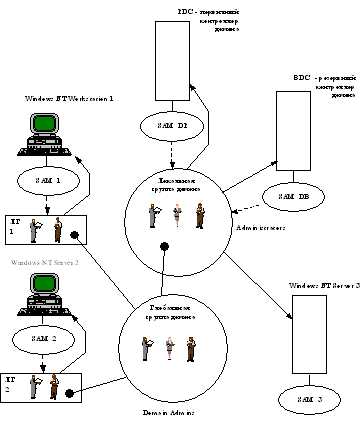
Рис. 5.1. Пример глобальной группы
Существует три типа встроенных глобальных групп: администратор домена (Domain Admins), пользователи домена (Domain Users) и гости домена (Domain Guests). Эти группы изначально являются членами локальных групп администраторов, пользователей и гостей соответственно.
Необходимо использовать встроенные группы там, где только это возможно. Рекомендуется формировать группы в следующей последовательности:
В учетном домене необходимо создать пользователей и добавить их к глобальным группам.
Включить глобальные группы в состав локальных групп ресурсных доменов.
Предоставить локальным группам необходимые права и разрешения.
Специальная группа - используется исключительно Windows NT Server для системного доступа. Специальные группы не содержат учетной информации пользователей и групп. Администраторы не могут приписать пользователей к этим группам. Пользователи либо являются членами этих групп по умолчанию (например, каждый пользователь является членом специальной группы Everyone), либо они становятся ими в зависимости от своей сетевой активности.
Существует 4 типа специальных групп:
Любой пользователь, который хочет получить доступ к разделяемому ресурсу по сети, автоматически становится членом группы Network. Пользователь, локально вошедший в компьютер, автоматически включается в группу Interactive. Один и тот же пользователь в зависимости от того, как он работает с компьютером, будет иметь разные права. Любой пользователь сети является членом группы Everyone. Администратор может назначить группе Everyone любые права. При этом администратор может предоставить любые права пользователю, не заводя на него учетной информации на своем компьютере. Группа Creator Owner содержит учетную информацию пользователя, который создал ресурс или владеет им.
В файловой системе NTFS разрешения группе Creator Owner даются на уровне каталога. Владелец любого каталога или файла, созданного в данном каталоге, получает разрешения, данные группе Creator Owner. Например, можно назначить какому-либо каталогу для членов группы Everyone разрешения Read (Чтение), а группе Creator Owner предоставить доступ Full Control (Полное управление). Любой пользователь, который создает файлы или подкаталоги в этом каталоге, будет иметь к ним доступ Full Control.
studfiles.net
локальная группа - это... Что такое локальная группа?
локальная группа local groupРусско-английский синонимический словарь. 2014.
- локальная геометрия
- локальная мощность
Смотреть что такое "локальная группа" в других словарях:
локальная группа — vietinė grupė statusas T sritis fizika atitikmenys: angl. local group vok. lokale Gruppe, f rus. локальная группа, f pranc. groupe local, m … Fizikos terminų žodynas
ЛОКАЛЬНАЯ ГРУППА ГАЛАКТИК — ЛОКАЛЬНАЯ ГРУППА ГАЛАКТИК, небольшая группа примерно из 30 ГАЛАКТИК, куда входит и наша Галактика, два Магеллановых Облака, Туманность Андромеды и спиральная галактика в созвездии Треугольника. Неравномерно распределены по эллипсовидному… … Научно-технический энциклопедический словарь
локальная группа пользователей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN local user groupLUG … Справочник технического переводчика
ЛИ ЛОКАЛЬНАЯ ГРУППА — аналитическая локальная группа, аналитическое многообразие Gнад полем k, полным относительно нек рого нетривиального абсолютного значения, снабженное отмеченным элементом е(единицей), открытым подмножеством и парой аналитич. отображений… … Математическая энциклопедия
Локальная топологическая группа — Локальная топологическая группа топологическая группа, в которой групповые операции определены лишь для элементов, достаточно близких к единице. Введение локальных топологических групп было инспирировано изучением локальной структуры… … Википедия
Локальная популяция — * лакальная папуляцыя * local polulation группа особей одного вида, проживающая на территории, в пределах которой они в основном спариваются между собой. Сином термина «локальная популяция» являются также термины «дим» и «менделевская популяция» … Генетика. Энциклопедический словарь
ГРУППА СУСЛОВИЕМ КОНЕЧНОСТИ — группа, элементы или подгруппы к рой удовлетворяют тому или иному условию конечности. Под условием конечности в теории групп понимается любое такое свойство, присущее всем конечным группам, что существуют бесконечные группы, к рые им не обладают … Математическая энциклопедия
Локальная теорема — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
ГРУППА — один из основных типов алгебраических систем. Теория Г. изучает в самой общей форме свойства алгебраич. операций, наиболее часто встречающихся в математике и ее приложениях (примеры таких операций умножение чисел, сложение векторов,… … Математическая энциклопедия
ГРУППА С ОДНОЗНАЧНЫМ ИЗВЛЕЧЕНИЕМ КОРНЯ — R группа группа, у к рой из равенства следует , где х, у любые элементы группы, п любое натуральное число. Группа Gтогда и только тогда является R группой, когда она без кручения и такова, что нз следует для любых п натурального числа п. R группа … Математическая энциклопедия
ЛОКАЛЬНАЯ ТОПОЛОГИЧЕСКАЯ ГРУППА — топологическая группа, в к рой групповые операции определены лишь для элементов, достаточно близких к единице. Введение Л. т. г. было инспирировано изучением локальной структуры топологич. групп (т. е. их структуры в сколь угодно малой… … Математическая энциклопедия
synonymum_ru_en.academic.ru
Локальная топологическая группа | Математика
Локальная топологическая группа — топологическая группа, в которой групповые операции определены лишь для элементов, достаточно близких к единице. Введение локальных топологических групп было инспирировано изучением локальной структуры топологических групп (т. е. их структуры в сколь угодно малой окрестности единицы).
Примером локальной топологической группы может служить любая окрестность единицы топологической группы . В теории локальных топологических групп принципиальным является вопрос о том, насколько общий характер имеет этот пример, т. е. является ли всякая локальная топологическая группа локально изоморфной некоторой топологической группе. В общем случае ответ отрицателен, но в важном частном случае конечномерных локальных групп Ли — положителен.
Как и в теории топологических групп, в теории локальных топологических групп можно определить понятия (локальных) подгрупп, нормальных делителей, смежных классов, факторгрупп.
Пусть $ G $ — топологическое пространство, $ e $ — некоторый его элемент, $ \Theta $ и $ \Omega $ — некоторые открытые подмножества в $ G $ и $ G\times G $ соответственно, $ e\in\Theta $ и $ i : \Theta\to G $, $ m:\Omega\to G $ — некоторые непрерывные отображения. Тогда система $ (G, e, \Theta, \Omega, i, m) $ является локальной топологической группой, если выполнены условия:
- $ (e,g) $ и $ (g,e)\in \Omega $ для любого $ g\in G $ и $ m(e, g) = m(g,e)=g $;
- если $ g,h,t\in G $ и $ (g, h), (h, t), (m(g, h), t), (g, m(h, t))\in \Omega $, то $ m(m(g, h), t) = m(g,m(h,t)) $;
- $ (g, i(g)) $ и $ (i(g), g)\in \Omega $ для любого $ g\in\Theta $ и $ m(g, i(g)) = m(i(g), g) = e $.
Обычно локальную топологическую группу $ (G, e, \Theta, \Omega, i, m) $ обозначают просто через $ G $; элемент $ m(g, h) $ обозначают через $ gh $ и называется произведением $ g $ и $ h $; элемент $ i(g) $ обозначают через $ g^{-1} $ и называется обратным к $ g $; элемент е называется единицей локальной топологической группы $ G $. Если $ (g, h)\in \Omega $, то говорят, что произведение $ g $ и $ h $ определено; если $ g\in\Theta $, то говорят, что для $ g $ определен обратный элемент.
Эти (определенные не для любых элементов) операции на $ G $ индуцируют структуру локальной топологической группы на любой окрестности единицы $ e $ в $ G $.
Связанные определенияПравить
Пусть $ G_1 $ и $ G_2 $ — две локальные топологические группы
Локальным гомоморфизмом $ G_1 $ в $ G_2 $ называется, такое непрерывное отображение $ h $ некотирой окрестности $ U_1 $ единицы $ e_1 $ локальной топологической группы $ G_1 $ в некоторую окрестность $ U_2 $ единицы $ e_2 $ локальной топологической группы $ G_2 $, что $ h(e_1) = e_2 $ и для любых элементов $ g, h\in U_1 $, произведение которых в $ G_1 $ определено, произведение элементов $ f(g) $ и $ f (h) $ в $ G_2 $ также определено и $ f(gh) = f(g) f(h) $. Два локальных гомоморфизма $ G_1 $ в $ G_2 $ называют эквивалентными, если они совпадают в некоторой окрестности единицы локальной топологической группы $ G_1 $. Пусть локальный гомоморфизм $ h $ является гомеоморфизмом окрестностей $ U_1 $ и $ U_2 $, а обратное отображение $ U_2\to U_1 $ является локальным гомоморфизмом $ G_2 $ в $ G_1 $. Тогда h называется локальным изоморфизмом $ G_1 $ в $ G_2 $. Две локальных топологических групп между которыми существует локальный изоморфизм, называются локально изоморфными. Например, любая локальная топологическая группа локально изоморфна любой своей окрестности единицы.
ru.math.wikia.com