Функции простые: Примеры графиков простых функций на плоскости
Содержание
Полная таблица производных элементарных функций
Поможем понять и полюбить математику
Начать учиться
184.3K
Самый частый вопрос, который возникает у старшеклассников на уроках алгебры, звучит примерно так: «А нам это в жизни пригодится?». Отвечаем: пригодится! Математика тесно связана с физикой, которая описывает окружающий нас мир. И формулы из таблицы производных основных элементарных функций тоже имеют практический смысл.
Что такое производная и зачем она нужна
Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:
Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю. |
Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.
Процесс нахождения производной называется дифференцированием.
Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке. В первую неделю она держалась каждый день по 10 секунд, но начиная со второй недели смогла стоять в планке с каждым днем на 3 секунды дольше. Успехи Маши можно описать следующими графиками:
Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.
у = 10
у′ = 0
Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.
у = 10 + 3х
Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1, а также по правилам вычисления производных (c*f(x))’=cf'(x) и (f(x)+g(x))’=f'(x)+g'(x).
у = 10 + 3х
у′ = 0 + 3
у′ = 3
Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.
Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций. Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.
Быстрее освоить производные поможет
обучение на курсах по математике в онлайн-школе Skysmart.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Производные основных элементарных функций
Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Поэтому приведем стандартную таблицу производных.
Функция f (x) | Производная f’ (х) |
|---|---|
С (т. | 0 |
х | 1 |
xn | nxn-1 |
√x | 1/(2√x) |
sin x | cos x |
cos x | -sin x |
tg x | 1/cos2(х) |
ctg x | -1/sin2x |
ex | ex |
ax | ax * ln a |
ln x | 1/x |
logax | 1/(x * ln a) |
Элементарные функции можно складывать, умножать друг на друга, находить их разность или частное — словом, выполнять любые математические операции. Но для этого существуют определенные правила.
Но для этого существуют определенные правила.
Общие правила дифференцирования
Для решения задач на дифференцирование нужно запомнить (или записать в шпаргалку) пять несложных формул:
(c ⋅ f)′ = c ⋅ f′
(u + v)′ = u′ + v′
(u — v)′ = u′ — v′
(u ⋅ v)′ = u′v + v′u
(u/v)’ = (u’v — v’u)/v2
В данном случае u, v, f — это функции, а c — константа (любое число).
С константой все просто — ее можно смело выносить за знак производной. Специально запоминать придется лишь формулы, где требуется разделить одну функцию на другую или перемножить их и найти производную от результата.
Например: требуется найти производную функции y = (5 ⋅ x3).
y′ = (5 ⋅ x3)′
Вспомним, что константу, а в данном случае это 5, можно вынести за знак производной:
y′ = (5 ⋅ x3)’ = 5 ⋅ (x3)′ = 5 ⋅ 3 ⋅ х3-1 = 15х2
Попробуйте самостоятельно решить эти примеры. Правильные ответы найдете в конце статьи:
Правильные ответы найдете в конце статьи:
Правила дифференцирования сложных функций
Конечно, далеко не все функции выглядят так, как в вышеуказанной таблице. Как быть с дифференцированием, например, вот таких функций: y = (3 + 2x2)4?
Сложной функцией называют такое выражение, в котором одна функция словно вложена в другую. Производную сложной функции f(y) можно найти по следующей формуле: (f(y))′ = f′(y) ⋅ y′. Другими словами, нужно умножить производную, условно говоря, внешней функции на производную внутренней. |
Пример 1
Найдем производную функции y(x) = (3 + 2x2)4.
Заменим 3 + 2x2 на u и тогда получим y = u4.
Согласно приведенному выше правилу дифференцирования сложных функций у нас получится:
y = y′u ⋅ u′x = 4u3 ⋅ u’x
А теперь выполним обратную замену и подставим исходное выражение:
4u3 ⋅ u′x = 4 (3 + 2x2)3 ⋅ (3 + 2x2)′ = 16 (3 + 2x2)3 ⋅ х
Пример 2
Найдем производную для функции y = (x3 + 4) cos x.
Для дифференцирования этой функции воспользуемся формулой (UV)′ = U′V + V′U.
y′ = (x3 + 4)′ ⋅ cos x + (x3 + 4) ⋅ cos x′ = 3x2 ⋅ cos x + (x3 + 4) ⋅ (-sin x) = 3x2 ⋅ cos x – (x3 + 4) ⋅ sin x
Ответы на задания
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Яна Кононенко
К предыдущей статье
Параллельность прямых
К следующей статье
Сколько стоят занятия с репетитором
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Найти производную: алгоритм и примеры решений
- Таблица производных простых функций
- Правила дифференцирования
- Пошаговые примеры — как найти производную
- Найти производные самостоятельно, а затем посмотреть решения
- Продолжаем искать производные вместе
Операция отыскания производной называется дифференцированием.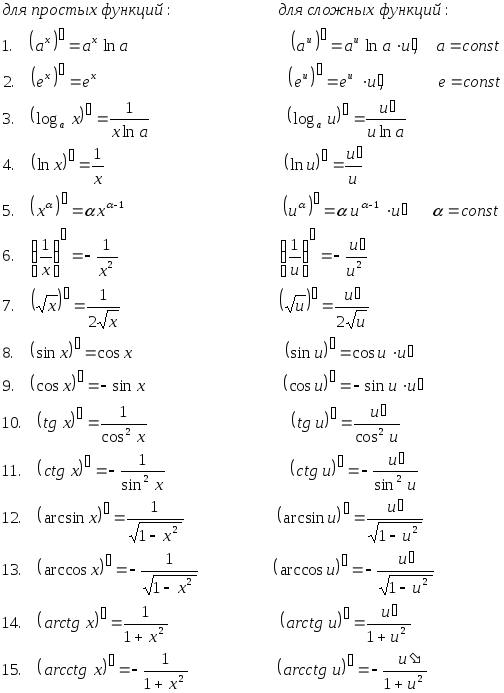
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной
как предела отношения приращения к приращению аргумента появились таблица производных и
точно определённые правила дифференцирования. Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную, надо выражение под знаком штриха разобрать на составляющие
простые функции и определить, какими действиями (произведение, сумма, частное)
связаны эти функции. Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования. Таблица производных и
Таблица производных и
правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
.
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу.
Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
.
Пример 2. Найти производную функции
.
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
| 12. Производная арктангенса | |
13. Производная арккотангенса Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.
Правило 2. Если функции
и
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной:
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
и
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций».
Здесь же (далее) — более простые примеры на производную произведения и частного, на которых Вы увереннее освоите алгоритмы вычислений.
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме
и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она
выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных,
но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое
u‘v, в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной
функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде , то
следуйте на занятие «Производная суммы дробей со степенями и корнями».
Если же перед Вами задача вроде ,
то Вам на занятие «Производные простых тригонометрических функций».
Пример 3. Найти производную функции
.
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель.
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем
требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где
сплошное нагромождение корней и степеней, как, например, ,
то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями».
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других
тригонометрических функций, то есть, когда функция имеет вид вроде ,
то Вам на урок «Производные простых тригонометрических функций».
Нет времени вникать в решение? Можно заказать работу!
Пройти тест по теме Производная, дифференциал и их применение
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на :
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 7. Найти производную функции
.
Правильное решение и ответ.
Пример 8. Найти производную функции
.
Правильное решение и ответ.
Пример 9. Найти производную функции
, где a и b — константы.
Правильное решение и ответ.
Пример 10. Найти производную функции
.
Правильное решение и ответ.
Пример 11. Найти производную функции
.
Правильное решение и ответ.
Ещё больше домашних заданий на нахождение производных
Пример 12. Найти производную функции
.
Решение. Применяя правила вычисления производной алгебраической суммы функций, вынесения постоянного множителя за знак производной и формулу производной степени (в таблице производных — под номером 3), получим
.
Пример 13. Найти производную функции
Решение. Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим
Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим
Пример 14. Найти производную функции
Решение. Как и в примерах 4 и 6, применим правило дифференцирования частного:
Теперь вычислим производные в числителе и перед нами уже требуемый результат:
Пример 15.Найти производную функции
Шаг1. Применяем правило дифференцирования суммы:
Шаг2. Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных — номер 5):
Шаг3. В частном знаменатель — также корень, только не квадратный. Поэтому преобразуем этот корень в степень:
и далее дифференцируем частное, не забывая, что число 2 в первом слагаемом числителя —
это константа, производная которой равна нулю, и, следовательно всё первое слагаемое равно нулю:
Корень из константы, как не трудно догадаться, является также константой, а производная константы, как мы знаем из таблицы производных, равна нулю:
,
а производная, требуемая в условии задачи:
Ещё больше домашних заданий на нахождение производных
Нет времени вникать в решение? Можно заказать работу!
Напоминаем, что чуть более сложные примеры на производную произведения и частного — в статьях «Производная произведения и частного функций» и
«Производная суммы дробей со степенями и корнями».
Также настоятельно рекомендуем изучить производную сложной функции.
| Назад | Листать | Вперёд>>> |
Пройти тест по теме Производная, дифференциал и их применение
Поделиться с друзьями
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритмы и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Уравнение касательной и уравнение нормали к графику функции
- Правило Лопиталя
- Частные производные
простая функция в nLab
Пропустить навигационные ссылки |
Домашняя страница |
Все страницы |
Последние версии |
Обсудить эту страницу |
Простые функции
- Идея
- Определения
- Интеграция
Идея
Простые функции (почти) самое основное понятие измеримой функции в теории меры. Учитывая меру, легко определить интеграл простой функции, и мы распространяем это на более общие функции по непрерывности.
Учитывая меру, легко определить интеграл простой функции, и мы распространяем это на более общие функции по непрерывности.
Определения
Пусть XX — измеримое пространство. Мы можем захотеть, чтобы XX был снабжен некоторыми дополнительными данными; если XX — пространство мер, то данных достаточно. Однако для самых основных определений достаточно, чтобы XX было просто измеримым пространством. Это область наших простых функций.
Другим необходимым данным является кодовая область KK простых функций, которую мы в конечном итоге захотим сделать как минимум банаховым пространством над действительными числами. (В простейшем примере KK — это само ℝ\mathbb{R} или, возможно, пространство ℂ\mathbb{C} комплексных чисел.) Мы считаем KK измеримым пространством, используя его борелевские множества.
Определение
Измеримая функция от XX до KK является простой , если ее область значений конечна.
Поскольку простая функция ff измерима, а одноэлементная функция борелевская, каждый слой ff является измеримым множеством в XX; функция ff задается (конечным числом) непустых слоев и их (одноэлементных) образов. Это предлагает другой взгляд на простые функции:
Это предлагает другой взгляд на простые функции:
Определение
Простая функция от XX до KK является формальной KK-линейной комбинацией измеримых подмножеств XX. 9n таких сумм.)
Однако наивное понятие равенства линейных комбинаций тоньше, чем равенство соответствующих функций, поэтому мы должны объединить Определение с определением равенства:
Определение
Две простые функции от XX до KK, в смысле определения равны , если их соответствующие функции от XX до KK равны как функции.
Тогда у нас есть каноническая биекция между множеством простых функций из определения и множеством классов эквивалентности простых функций из определения .
Возможно, даже это не совсем правильное понятие равенства, поскольку функции могут быть равными для целей интеграции, но не быть равными буквально. Если XX оснащен σ\sigma-идеалом нулевых множеств (или δ\дельта-фильтром полных множеств), то мы можем рассмотреть еще более грубое понятие равенства:
Определение
Две простые функции в смысле определения или определения, почти равны , если они (или их соответствующие функции) равны почти всюду.
Иногда мы хотим ограничить внимание теми простыми функциями, которые, как мы ожидаем, будут иметь конечный интеграл. Если XX снабжен идеалом ограниченных множеств (которые в пространстве с мерой являются множествами с конечной мерой), то мы можем сделать это:
Определение
Определение такое, что слой над каждым ненулевым числом ограничен, или, что то же самое (в смысле определения ), формальная линейная комбинация ограниченных измеримых множеств.
В некоторых подходах к теории меры начинают с δ\дельта-кольца измеримых множеств, которые могут быть переинтерпретированы как ограниченные множества в порожденной σ\sigma-алгебре относительно измеримых множеств, а затем простые функции автоматически будет иметь ограниченную поддержку.
Наконец, есть еще одно полезное ограничение (и небольшое обобщение) простых функций, применимое, когда KK упорядочен:
Определение
A положительная простая функция 9+-линейная комбинация.
Интегрирование
Пусть XX снабжено мерой µ\mu, поэтому (X,µ)(X,\mu) является пространством с мерой. (В частности, XX имеет структуру, необходимую для всех приведенных выше определений, включая определения и .)
Если ff — простая функция от XX до KK, то мы хотим определить интеграл от ff. В общем, это немного сложно, но легко, если ff положительно или имеет ограниченный носитель. Легче всего записать определение, если мы думаем о простых функциях, используя Definition. Тогда имеем:
Определение
Интеграл простой функции ff, представленный линейной комбинацией ∑iciAi\sum_i c_i A_i, равен ∑iciµ(Ai)\sum_i c_i \mu(A_i).
Предложение
Интеграл положительной простой функции всегда существует (но может быть бесконечным). Она конечна, если µ\mu — конечная мера, и положительна (возможно, 00 или ∞\infty), если µ\mu — положительная мера. Кроме того, если µ \ mu положительно, то всегда существует интеграл от расширенной положительной простой функции.
(Однако интеграл расширенной положительной простой функции по конечной положительной мере не обязательно должен быть конечным.)
Предложение
Интеграл простой функции с ограниченным носителем всегда существует и конечен (будучи конечным линейным комбинация конечных чисел).
Предложение
Две (положительные или с ограниченным носителем) простые функции ff и gg почти равны (относительно µ\mu) тогда и только тогда, когда интеграл от f−gf — g равен нулю. 91-норма простой функции представляет собой интеграл от ее поточечной нормы (которая является положительной простой функцией для ℝ\mathbb{R}) по модулю меры µ\mu (которая является положительной мерой):
‖f‖1≔∫‖f(x)‖|µ(dx)|. {\|f\|}_1 \coloneqq \int {\|f(x)\|} {|\mu(\mathrm{d}x)|} .
В этом контексте мы обычно начинаем с положительной меры µ\mu; в этом случае, конечно, нет нужды утруждать себя взятием абсолютного значения µ\mu.
Предложение
91.
Таким образом, мы можем определить интеграл любой абсолютно интегрируемой функции.
Для этого могут существовать некоторые технические требования. Я постараюсь проверить это.
Последняя редакция: 9 января 2013 г., 00:33:08.
См. историю этой страницы для получения списка всех вкладов в нее.
Простые и элементарные функции «Математик без извинений»
Теперь мы познакомимся с двумя классами функций, с которыми очень легко работать. Как обычно, мы работаем в некотором измеримом пространстве.
Во-первых, у нас есть «простые функции». Такая функция описывается путем выбора конечного числа попарно непересекающихся измеримых множеств и соответствующего набора из конечных действительных чисел. Мы используем их, чтобы определить функцию, объявив if , и если нет ни в одном из . Самый простой пример — характеристическая функция измеримой функции. Любая другая простая функция может быть записана как
Любая простая функция измерима, поскольку прообраз представляет собой объединение всех соответствующих им , и поэтому измерима.
Несложно проверить, что произведение и сумма любых двух простых функций сама по себе является простой функцией — заданы функции и , у нас есть и . Еще проще увидеть, что любое скалярное кратное простой функции просто — . Таким образом, совокупность простых функций образует подалгебру алгебры измеримых функций.
«Элементарные функции» аналогичны простым функциям. Мы немного ослабим условия, допуская счетно бесконечное число измеримых множеств и соответствующих значений.
Почему нас интересуют простые функции? Как оказалось, каждая измеримая функция может быть аппроксимирована простыми функциями! То есть по любой измеримой функции мы можем найти последовательность из простых функций, поточечно сходящихся к .
Чтобы увидеть это, сначала разбейте его на положительную и отрицательную части и . Если мы можем аппроксимировать любую неотрицательную измеримую функцию поточечно возрастающей последовательностью неотрицательных простых функций, то мы можем аппроксимировать каждый из и , а разность этих рядов аппроксимирует . Итак, не ограничивая общности, будем считать, что неотрицательно.
Итак, не ограничивая общности, будем считать, что неотрицательно.
Итак, вот как мы определим простые функции:
То есть, чтобы определить, мы разбиваем неотрицательные действительные числа на куски ширины, и в каждом из этих кусочков мы округляем значения вниз в меньшую сторону. конечная точка. Если , мы округляем до . Могут быть только значения для , и каждое из них соответствует измеримому набору. Значение соответствует набору
, а значение соответствует набору . Таким образом, это действительно простая функция.
Итак, сходится ли последовательность поточечно к ? Ну а если, то для всех. С другой стороны, если тогда ; после этой точки и оба находятся в пределах среза шириной , и так далее. Таким образом, учитывая достаточно большое значение, мы можем установить любую желаемую границу . Таким образом, последовательность возрастает поточечно до функции .
Но это еще не все! Если ограничено сверху некоторым целым числом , то последовательность сходится равномерно к .
 е. константа, любое число)
е. константа, любое число)