Иллюстрированный самоучитель по цифровой графике. Как найти размер файла формула
Теория и разбор 9 задания ЕГЭ по информатике по теме Кодирование
Урок посвящен разбору задания 9 ЕГЭ по информатике
Объяснение заданий 9 ЕГЭ по информатике
9 тема характеризуется, как задания базового уровня сложности, время выполнения – примерно 5 минут
Кодирование текстовой информации
I = n * i
где:
Кодирование графической информации
Рассмотрим некоторые понятия и формулы, необходимые для решения ЕГЭ по информатике данной темы.
- Пиксель – это наименьший элемент растрового изображения, который имеет определенный цвет.
- Разрешение – это количество пикселей на дюйм размера изображения.
- Глубина цвета — это количество битов, необходимое для кодирования цвета пикселя.
- Если глубина кодирования составляет i битов на пиксель, код каждого пикселя выбирается из 2i возможных вариантов, поэтому можно использовать не более 2i различных цветов.
- N — количество цветов
- i — глубина цвета
- В цветовой модели RGB (красный (R), зеленый (G), синий (B)): R (0..255) G (0..255) B (0..255) -> получаем 28 вариантов на каждый из трех цветов.
- R G B: 24 бита = 3 байта — режим True Color (истинный цвет)
- I — объем памяти, требуемый для хранения изображения
- M — ширина изображения в пикселях
- N — высота изображения в пикселях
- i — глубина кодирования цвета или разрешение
- где N – количество пикселей (M * N) и i – глубина кодирования цвета (разрядность кодирования)
- Следует также помнить формулы преобразования:
Формула для нахождения количества цветов в используемой палитре:
i = log2N
Найдем формулу объема памяти для хранения растрового изображения:
I = M * N * i
где:
Или можно формулу записать так:
I = N * i битов
* для указания объема выделенной памяти встречаются разные обозначения (V или I).
1 Мбайт = 220 байт = 223 бит,1 Кбайт = 210 байт = 213 бит
Кодирование звуковой информации
- Оцифровка или дискретизация – это преобразование аналогового сигнала в цифровой код.
- T – интервал дискретизации (измеряется в с)
- ƒ — частота дискретизации (измеряется в Гц, кГц)
- Частота дискретизации определяет количество отсчетов, т.е. отдельных значений сигнала, запоминаемых за 1 секунду. Измеряется в герцах, 1 Гц (один герц) – это один отсчет в секунду, а, например, 7 кГц – это 7000 отсчетов в секунду.
- Разрядность кодирования (глубина, разрешение) — это число битов, используемое для хранения одного отсчёта.
- Получим формулу объема звукового файла:
- I — объем
- β — глубина кодирования
- ƒ — частота дискретизации
- t — время
- S — количество каналов

Дискретизация, объяснение задания 9 ЕГЭ
* Изображение взято из презентации К. Полякова
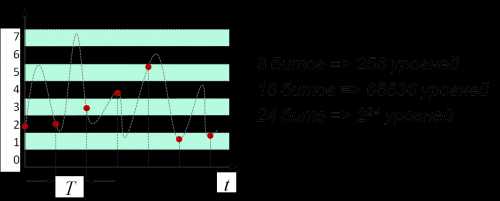
Разрядность кодирования
* Изображение взято из презентации К. Полякова
Для хранения информации о звуке длительностью t секунд, закодированном с частотой дискретизации ƒ Гц и глубиной кодирования β бит требуется бит памяти:
I = β * ƒ * t * S
S для моно = 1, для стерео = 2, для квадро = 4
Пример: при ƒ=8 кГц, глубине кодирования 16 бит на отсчёт и длительности звука 128 с. потребуется:
✍ Решение:I = 8000*16*128 = 16384000 битI = 8000*16*128/8 = 23 * 1000 * 24 * 27 / 23 = 214 / 23 =211 == 2048000 байт
Определение скорости передачи информации
- Канал связи всегда имеет ограниченную пропускную способность (скорость передачи информации), которая зависит от свойств аппаратуры и самой линии связи(кабеля)
- I — объем информации
- v — пропускная способность канала связи (измеряется в битах в секунду или подобных единицах)
- t — время передачи
Объем переданной информации I вычисляется по формуле:
I = V * t
* Вместо обозначения скорости V иногда используется q* Вместо обозначения объема сообщения I иногда используется Q
Скорость передачи данных определяется по формуле:
V = I/t
и измеряется в бит/с
Егифка ©:

Решение заданий 9 ЕГЭ по информатике
Тема: Кодирование изображений:
ЕГЭ по информатике 2017 задание 9 ФИПИ вариант 1 (Крылов С.С., Чуркина Т.Е.):Какой минимальный объем памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 160 х 160 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
✍ Решение:- Используем формулу нахождения объема:
- Подсчитаем каждый сомножитель в формуле, стараясь привести числа к степеням двойки:
- M x N:
Результат: 25
Детальный разбор задания 9 ЕГЭ по информатике предлагаем посмотреть в видео:
Тема: Кодирование изображений:
ЕГЭ по информатике задание 9.2 (источник: 9.1 вариант 11, К. Поляков):Рисунок размером 128 на 256 пикселей занимает в памяти 24 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
✍ Решение:- По формуле объема файла изображения имеем:
- где M * N — общее количество пикселей. Найдем это значение, используя для удобства степени двойки:
Количество цветов = 2i
i = I / (M*N)
Результат: 64
Смотрите видеоразбор задания:
Тема: Кодирование изображений:
ЕГЭ по информатике задание 9.3 (источник: 9.1 вариант 24, К. Поляков):- По формуле объема файла изображения имеем:
- i можно найти, зная количество цветов в палитре:
где N — общее количество пикселей,а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)
количество цветов = 2i
Результат: 24
Подробный разбор 9 задания ЕГЭ смотрите на видео:
Тема: Кодирование изображений:
ЕГЭ по информатике задание 9.4 (источник: 9.1 вариант 28, К. Поляков, С. Логинова):- По формуле объема файла изображения имеем:
- В такого рода задачах необходимо учесть, что уменьшение разрешения в 2 раза, подразумевает уменьшение в 2 раза пикселей отдельно по ширине и по высоте. Т.е. в целом N уменьшается в 4 раза!
- Составим систему уравнений на основе имеющихся сведений, в которой первое уравнение будет соответствовать данным до преобразования файла, а второе уравнение — после:
где N — общее количество пикселей или разрешение,а i — глубина цвета (количество бит, выделенное на 1 пиксель)
\[ I= \frac {N}{4} * 4* \frac {42}{N} \]
Результат: 42
Тема: Кодирование изображений:
ЕГЭ по информатике задание 9.5 (источник: 9.1 вариант 30, К. Поляков, С. Логинова):Изображение было оцифровано и сохранено в виде растрового файла. Получившийся файл был передан в город А по каналу связи за 72 секунды. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 3 раза выше, чем канала связи с городом А.Сколько секунд длилась передача файла в город Б?
✍ Решение:- По формуле скорости передачи файла имеем:
- По формуле объема файла изображения имеем:
- Для данной задачи, необходимо уточнить, что разрешение на самом деле имеет два сомножителя (пикселей по ширине * пикселей по высоте). Поэтому при увеличении разрешения в два раза, увеличатся оба числа, т.е. N увеличится в 4 раза вместо двух.
- Изменим формулу получения объема файла для города Б:
- Для города А и Б заменим значения объема в формуле для получения скорости:
- Подставим значение скорости из формулы для города А в формулу для города Б:
- Выразим t:
где I — объем файла, а t — время
где N — общее количество пикселей или разрешение,а i — глубина цвета (количество бит, выделенное на 1 пиксель)
\[ I= \frac {2*N * i}{3} \]
Город А:
\[ V= \frac {N*i}{72} \]
Город Б:
\[ 3*V= \frac{\frac {4*N*i}{3}}{t} \]
или:
\[ t*3*V= \frac {4*N*i}{3} \]
\[ \frac {t*3*N*i}{72}= \frac {4*N*i}{3} \]
Результат: 32
Другой способ решения смотрите в видеоуроке:
Тема: Кодирование изображений:
ЕГЭ по информатике задание 9.6 (источник: 9.1 вариант 33, К. Поляков):Камера делает фотоснимки размером 1024 х 768 пикселей. На хранение одного кадра отводится 900 Кбайт.Найдите максимально возможное количество цветов в палитре изображения.
✍ Решение:- Количество цветов зависит от глубины кодирования цвета, которая измеряется в битах. Для хранения кадра, т.е. общего количества пикселей выделено 900 Кбайт. Переведем в биты:
\[ \frac {225 * 2^{15}}{3 * 2^{18}} = \frac {75}{8} \approx 9 \]
9 бит на 1 пиксельРезультат: 512
Смотрите подробное решение на видео:
Тема: Кодирование звука:
ЕГЭ по информатике 2017 задание 9 ФИПИ вариант 15 (Крылов С.С., Чуркина Т.Е.):На студии при четырехканальной (квадро) звукозаписи с 32-битным разрешением за 30 секунд был записан звуковой файл. Сжатие данных не производилось. Известно, что размер файла оказался 7500 Кбайт.
С какой частотой дискретизации (в кГц) велась запись? В качестве ответа укажите только число, единицы измерения указывать не нужно.
✍ Решение:- По формуле объема звукового файла получим:
- Из задания имеем:
I = β * t * ƒ * S
\[ ƒ = \frac {I}{S*B*t} = \frac {7500 * 2^{10} * 2^2 бит}{2^7 * 30}Гц = \frac { 750 * 2^6}{1000}КГц = 2^4 = 16 \]
24 = 16 КГц
Результат: 16
Для более детального разбора предлагаем посмотреть видео решения данного 9 задания ЕГЭ по информатике:
Тема: Кодирование изображений:
9 задание. Демоверсия ЕГЭ 2018 информатика:Автоматическая фотокамера производит растровые изображения размером 640×480 пикселей. При этом объём файла с изображением не может превышать 320 Кбайт, упаковка данных не производится.Какое максимальное количество цветов можно использовать в палитре?
✍ Решение:- По формуле объема файла изображения имеем:
- Посмотрим, что из формулы нам уже дано:
I = N * i
где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)
количество цветов = 2i
\[ i = \frac {I}{N} = \frac {320 * 2^{13}}{75 * 2^{12}} \approx 8,5 бит \]
Результат: 256
Подробное решение данного 9 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Тема: Кодирование звука:
ЕГЭ по информатике задание 9.9 (источник: 9.2 вариант 36, К. Поляков):Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А.
Сколько секунд длилась передача файла в город A? В ответе запишите только целое число, единицу измерения писать не нужно.
✍ Решение:- Для решения понадобится формула нахождения скорости передачи данных формулы:
- Вспомним также формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся города Б (про А практически ничего не известно):
V = I/t
I = β * ƒ * t * s
где:I — объемβ — глубина кодированияƒ — частота дискретизацииt — времяS — кол-во каналов (если не указывается, то моно)
\[ t_А = \frac {15}{2} * 3 * 4 \]
90 секундРезультат: 90
Подробное решение смотрите на видео:
Тема: Кодирование звука:
ЕГЭ по информатике задание 9.10 (источник: 9.2 вариант 43, К. Поляков):Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 30 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось.
Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.
✍ Решение:- Вспомним формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся первого состояния файла, затем второго состояния — после преобразования:
I = β * ƒ * t * S
I — объемβ — глубина кодированияƒ — частота дискретизацииt — времяS -количество каналов
Результат: 20
Смотрите видеоразбор данной задачи:
Тема: Кодирование звуковых файлов:
ЕГЭ по информатике задание 9.11 (источник: 9.2 вариант 72, К. Поляков):Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 100 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 4 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд.
Во сколько раз скорость (пропускная способность канала) в город Б больше пропускной способности канала в город А?
✍ Решение:- Вспомним формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся файла, переданного в город А, затем преобразованного файла, переданного в город Б:
I = β * ƒ * t * S
I — объемβ — глубина кодированияƒ — частота дискретизацииt — время✎ 1 способ решения:
Ответ: 5 ✎ 2 способ решения:
\[ \frac {V_Б}{V_А} = \frac {3/_4 * I}{15} * \frac {100}{I} = \frac {3/_4 * 100}{15} = \frac {15}{3} = 5 \]
(((3/4) * I) / 15) * (100 / I)= (3/4 * 100) / 15 = 15/3 = 5Результат: 5
Подробный видеоразбор задания:
Тема: Кодирование звука:
ЕГЭ по информатике задание 9.12 (источник: 9.2 вариант 80, К. Поляков):Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится.
Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.
✍ Решение:- Вспомним формулу объема звукового файла:
- Для простоты расчетов пока не будем брать во внимание количество каналов. Рассмотрим, какие данные у нас есть, и какие из них необходимо перевести в другие единицы измерения:
I — объемβ — глубина кодированияƒ — частота дискретизацииt — времяS — количество каналов
Результат: 60
Смотрите подробное решение:
Тема: Скорость передачи данных:
ЕГЭ по информатике задание 9.13 (источник: 9.V вариант 5, К. Поляков):Скорость передачи данных через ADSL-соединение равна 128000 бит/с. Передача текстового файла через это соединение заняла 1 минуту. Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.
✍ Решение:- Вспомним формулу скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
Результат: 480000
Разбор 9 задания:
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 9.14 (источник: 9.V вариант 23, К. Поляков):У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 217 бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 216 бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 8 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных.
Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей?
✍ Решение:- Вспомним формулу скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
Результат: 1088
Подробный разбор смотрите на видео:
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 9.15 (источник: 9.V вариант 28, К. Поляков):Сколько секунд потребуется модему, передающему сообщения со скоростью 32000 бит/с, чтобы передать 16-цветное растровое изображение размером 800 x 600 пикселей, при условии, что в каждом байте закодировано максимально возможное число пикселей?
✍ Решение:- Вспомним формулу скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
Результат: 60
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 9.16 (источник: 9.V вариант 34, К. Поляков):Каково время (в минутах) передачи полного объема данных по каналу связи, если известно, что передано 9000 Мбайт данных, причем треть времени передача шла со скоростью 60 Мбит в секунду, а остальное время – со скоростью 90 Мбит в секунду?
✍ Решение:- Формула скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
1 Мбайт = 8 Мбит
Q = 9000 Мбайт * 8 = 72000 МбитРезультат: 15
Решение задания можно посмотреть и на видео:
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 9.17 (источник: 9.V вариант 43, К. Поляков):Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:А) Сжать архиватором, передать архив по каналу связи, распаковатьБ) Передать по каналу связи без использования архиватора.
Какой способ быстрее и насколько, если
- средняя скорость передачи данных по каналу связи составляет 218 бит в секунду,
- объем сжатого архиватором документа равен 20% от исходного,
- время, требуемое на сжатие документа – 7 секунд, на распаковку – 1 секунда?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.
Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.
✍ Решение:- Рассмотрим способ А:
- Сначала найдем объем документа, зная, что он составляет 20% от исходного:
Рассмотрим способ Б:
Результат: А120
Решение также можно посмотреть в видеоуроке:
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 9.18 (источник: 9.V вариант 72, К. Поляков):Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя способами:А) сжать архиватором-1, передать архив по каналу связи, распаковать;Б) сжать архиватором-2, передать архив по каналу связи, распаковать;
Какой способ быстрее и насколько, если
- средняя скорость передачи данных по каналу связи составляет 220 бит в секунду,
- объём документа, сжатого архиватором-1, равен 20% от исходного,
- на сжатие документа архиватором-1 требуется 15 секунд, на распаковку — 2 секунды,
- объём документа, сжатого архиватором-2, равен 10% от исходного,
- на сжатие документа архиватором-2 требуется 20 секунд, на распаковку — 4 секунды?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.
Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.
✍ Решение:- Рассмотрим способ А:
- Сначала найдем объем документа, зная, что он составляет 20% от исходного:
Рассмотрим способ Б:
Результат: Б9
Тема: Кодирование звука:
Государственный выпускной экзамен ГВЭ 2018 (информатика ГВЭ ФИПИ, задание 7):Производится двухканальная (стерео) цифровая звукозапись. Значение сигнала фиксируется 48 000 раз в секунду, для записи каждого значения используется 32 бит. Запись длится 5 минут, её результаты записываются в файл, сжатие данных не производится.
Какая из приведённых ниже величин наиболее близка к размеру полученного файла?
1) 14 Мбайт2) 28 Мбайт3) 55 Мбайт4) 110 Мбайт
✍ Решение:- По формуле объема звукового файла имеем:
Результат: 4
Подробное решение ГВЭ задания 7 2018 года смотрите на видео:
Тема: Кодирование звука:
Решение 9 задания ЕГЭ по информатике (диагностический вариант экзаменационной работы 2018 года, С.С. Крылов, Д.М. Ушаков):Производится двухканальная (стерео) звукозапись с частотой дискретизации 4 кГц и 64-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится.
Определите приблизительно размер получившегося файла (в Мбайтах). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 2.
✍ Решение:- По формуле объема звукового файла имеем:
Результат: 4
Видеоразбор задания:
labs.org.ru
Задачи по информатике информационный объем графического файла 15
Тема №8192
Здесь находится описание темы Задачи по информатике информационный объем графического файла 15, изучаемой по предмету Информатика. Ниже вы разберете ответы на все ваши разнообразные вопросы. Если представленный текст вам не помог, то вы смело можете задать свои вопросы ниже.
ИНФОРМАЦИОННЫЙ ОБЪЕМ ГРАФИЧЕСКОГО ФАЙЛА
Палитра (N) - количество используемых в наборе цветов.
Глубина цвета (I) - количество бит (двоичных разрядов), отводимых в видеопамяти под каждый пиксель.
Каждый цвет имеет свой уникальный двоичный код.
Код цвета пикселя содержит информацию о доле каждого базового цвета.
Число цветов, воспроизводимых на экране монитора (N), и число бит, отводимых под кодирование цвета одного пикселя (I), находится по формуле:
N=2I
Глубина цвета и количество отображаемых цветов
| Глубина цвета (I) | Количество отображаемых цветов (N) |
| 8 | 28=256 |
| 16 (High Color) | 216=65 536 |
| 24 (True Color) | 224=16 777 216 |
| 32 (True Color) | 232=4 294 967 296 |
V=K*I,
где V - информационный объем рисунка (файла), К - общее количество точек рисунка или разрешающая способность монитора, I - глубина цвета.
ЗАДАЧИ
Задача 1. Какой объем информации занимает черно-белое изображение размером 600 х 800?
Решение: 600 х 800 = 480 000 точек 480 000 точек х 1 бит = 480 000 бит
480 000 бит / 8 бит / 1024 байт ≈ 58, 59 Кбайт
Ответ: 58, 59 Кбайт
Задача 2. Сколько информации содержится в картинке экрана с разрешающей способностью 800х600 пикселей и 16 цветами?
Решение: Количество точек К=800х600=480000
Глубина цвета I=4 бита, т.к. 24=16
480000·4 = 1920000 бит = 240000 б= 234,375 Мб ≈ 0,23 Кб
Ответ: 0,23 Кб
Задача 3. Определить объем растрового изображения размером 200 х 200 и 256 цветами.
Решение: 200 х 200 х 8 бит = 320 000 бит / 8 бит / 1024 байт = 39,0625 Кбайт ≈ 39 Кбайт
Ответ: 39 Кбайт
Задача 4. Определить объем растрового изображения размером 600 х 800 при глубине цвета 24 бита.
Решение: 600 х 800 = 480 000 точек 480 000 точек х 24 бит = 11 520 000 бит
11 520 000 бит / 8 бит / 1024 байт = 1406,25 Кбайт / 1024 байт ≈ 1,37 Мбайт
Ответ: ≈ 1,37 Мбайт
Задача 5. Определить объем видеопамяти компьютера, который необходим для реализации графического режима монитора с разрешающей способностью 1024×768 и палитрой 65536 цветов.
Решение: N = 2i = 65536 i = 16 бит Количество точек изображения равно: 1024 х 768 = 786432
16 бит х 786432 = 12582912 бита / 8 бит / 1024 байт = 1536 Кбайт / 1024 байт = 1,5 М байта
Ответ: 1,5 М байта
Задача 6. Растровый файл, содержащий черно-белый рисунок, имеет объем 300 байт. Какой размер может иметь рисунок в пикселях?
Решение: Объем файла V=300б=2400бит. Рисунок черно-белый, значит, палитра состоит из двух цветов (черный, белый), т.е. N=2. Отсюда находим глубину цвета I= 1бит.
К=V/I=2400бит/1бит=2400 пикселей.
Ответ: Рисунок может состоять из 2400 пикселей.
Задача 7. Достаточно ли видеопамяти объемом 256 Кб для работы монитора в режиме 640х480 и палитрой из 16 цветов?
Решение: Палитра N = 16, следовательно, глубина цвета I = 4 бита (24=16).
Общее количество точек равно: 640 · 480 = 307200.
Информационный объем равен:
307200 · 4 бита = 1228800 бит = 153600 байт = 150 Кб
Ответ: видеопамяти достаточно, 150 Кб < 256 Кб
Задача 8. Определить максимально возможную разрешающую способность экрана монитора с диагональю 15" и размером точки экрана 0,28 мм.
Решение: Выразим размер диагонали в сантиметрах (1 дюйм = 2,54 см):
2,54 см · 15 = 38,1 см
Определим соотношение между высотой и шириной экрана для режима 1024х768 точек:
768 : 1024 = 0,75
Определим ширину экрана. Пусть ширина экрана равна L, тогда высота равна 0,75L.
По теореме Пифагора имеем:
L2 + (0,75L)2 = 38,12
1,5625L2 = 1451,61
L2 ≈ 929
L ≈ 30,5 см
Количество точек по ширине экрана равно:
305 мм : 0,28 мм = 1089
Ответ: Максимально возможным разрешением экрана монитора является 1024х768.
Задача 9. Сканируется цветное изображение размером 10х10 см. Разрешающая способность сканера 600 dpi и глубина цвета 32 бита. Какой информационный объем будет иметь полученный графический файл?
Решение: Разрешающая способность сканера 600 dpi (dot per inch - точек на дюйм) означает, что на отрезке длиной 1 дюйм сканер способен различить 600 точек.
Переведем разрешающую способность сканера из точек на дюйм (1 дюйм = 2,54 см) в точки на сантиметр:
600dpi : 2,54 ≈ 236 точек/см.
Следовательно, размер изображения в точках составит
2360х2360 точек.
Общее количество точек изображения равно:
2360 · 2360 = 5 569 600.
Информационный объем файла равен:
32 бита · 5569600 = 178 227 200 бит = 22278400 б = 21756 Кб ≈ 21 Мб
Ответ: 21 Мб.
Задания для самостоятельной работы
на определение информационного объем графического файла
1. Сколько цветов будет в палитре, если каждый базовый цвет кодировать в 6 битах?
2. Для хранения растрового изображения размером 1024х512 пикселей отвели 256 Кбайт памяти. Каково максимально возможное число цветов в палитре изображения?
3. Сколько памяти компьютера требуется для двоичного кодирования 256-цветного рисунка размером 10 х 10 точек?
4. Разрешение экрана монитора – 1024х768 точек, глубина цвета – 16 бит. Каков необходимый объем видеопамяти для данного графического режима?
5. Объем видеопамяти равен 512 Кбайт, разрешающая способность дисплея – 800х600. Какое максимальное количество цветов можно использовать при таких условиях?
6.Для кодирования одного пикселя используется 3 байта. Фотографию размером 2048 х 1536 пикселей сохранили в виде несжатого файла. Определите размер получившегося файла.
7. Объём видеопамяти равен 4 Мб, битовая глубина – 24, разрешающая способность дисплея – 640 х 480. Какое максимальное количество страниц можно использовать при этих условиях?
8. Для хранения изображения размером 128х128 точек выделено 4 Кбайт памяти. Определите, какое максимальное число цветов в палитре.
9.16-цветный рисунок содержит 500 байт информации. Из скольких точек он состоит?
10.Определить объем видеопамяти в Килобайтах для графического файла размером 640х480 пикселей и палитрой из 32 цветов
11.После преобразования графического изображения количество цветов уменьшилось с 256 до 32. Во сколько раз уменьшился объем занимаемой им памяти?
12. Несжатое растровое изображение размером 128 х 128 пикселей занимает 2 Кб памяти. Каково максимально возможное число цветов в палитре изображения?
13.Цветной сканер имеет разрешение 1024х512 точек на дюйм. Объем памяти, занимаемой просканированным изображением размером 2х4 дюйма, составляет около 8 Мбайт. Какова выраженная в битах глубина представления цвета сканера?
14.После преобразования растрового 256-цветного графического файла в черно-белый двуцветный формат его размер уменьшился на 70 байт. Каков был размер исходного файла в байтах?
15.В процессе преобразования растрового графического файла его объем уменьшился в 1,5 раза. Сколько цветов было в палитре первоначально, если после преобразования получено изображение того же разрешения в 256-цветной палитре?
Категория: Информатика | Добавил: (10.09.2016) Просмотров: 1 | Рейтинг: 0.0/0xn----8sbhepth3ca.xn--p1ai
Иллюстрированный самоучитель по цифровой графике › Объем файла пиксельной графики › Формула объема пиксельного файла [страница - 117] | Самоучители по графическим программам
Формула объема пиксельного файла
Это важная глава с практической точки зрения, поскольку объем пиксельного файла является критичным фактором при большом количестве графических документов. И разобраться в том, что формирует объем файла, совершенно необходимо для того, чтобы оптимально выбирать не только параметры пиксельного документа, но и форматы файлов.
Объем пиксельного файла – это тот объем информации, для хранения которого требуется соответствующий объем дискового пространства. Для того чтобы определить, может ли какой-либо носитель информации (например, такой "малобюджетный", как дискета) вместить тот или иной объем информации, необходим предварительный расчет ("прикидка") требуемого объема при устанавливаемых параметрах.
Создание фиксированной числовой матрицы предполагает простой расчет ее объема по параметрам пиксельной графики (геометрическим размерам, разрешению и глубине цвета). Никакие иные характеристики пиксельного изображения на объем числового массива влияния не оказывают. В данной главе представлена простая формула, которую используют любые программы, связанные с пиксельной графикой, а также специализированные программы, обслуживающие сканеры. Эта формула позволит, устанавливая параметры пиксельной графики, заранее, еще не сканируя или еще не создавая изображения, рассчитать объем файла.
Значительные объемы любых файлов стимулируют создание алгоритмов сжатия информации, в том числе и графической, полезным представляется знакомство с особенностями основных форматов графических файлов.
В данном разделе предстоит составить довольно простую формулу, которая позволит в дальнейшем рассчитывать объем файла.
ЗамечаниеСледует иметь в виду, что пока речь не идет о форматах, а только о совокупности битовых карт, которые занимают определенный объем дисковой или оперативной памяти.
Прежде всего разумно признать, что метафора объема пиксельного файла имеет реальные основания: площадь матрицы и совокупность битовых карт, уходящих в глубину, волей-неволей провоцируют представление об объемном теле, например параллелепипеде (рис. 10.1).
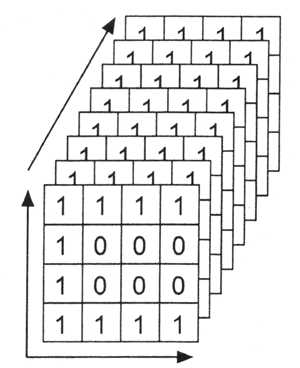 Рис. 10.1. Метафора объема пиксельного изображения
Рис. 10.1. Метафора объема пиксельного изображения
Объем такого тела, естественно, вычисляется путем перемножения его составляющих. Правда, у "виртуального" пиксельного параллелепипеда есть некоторые особенности.
Предположим, что необходимо рассчитать объем дискового пространства для хранения черно-белого тонового изображения размером 127x254 мм и разрешением 72 ppi.
Начнем с того, что значения длины, которую можно обозначить символом L, и ширины, которую можно обозначить символом W, необходимо представить в дюймах:
L = 127: 25.4 = 5 (дюймов)
W = 254: 25.4 = 10 (дюймов)
Площадь изображения, обозначим ее символом S, как всем известно, вычисляется перемножением этих величин:
S = L x W = 5 x 10 = 50 (квадратных дюймов).
Геометрическая площадь изображения содержит сетку дискретизации, поэтому следующим шагом необходимо вычислить общее количество пикселов. Для этого следует учесть, что величина разрешения, которую обозначим символом R, по определению – величина линейная, а дискретизация осуществляется по площади.
Информацию об определении разрешения см. в главе 7.
Следовательно, сначала необходимо вычислить количество пикселов в квадратном дюйме:
N1 = R2 = 72 х 72 = 5184 (пикселов).
А поскольку площадь изображения составляет не один квадратный дюйм, то общее количество пикселов будет равно:
N = N1 х S= 5184 х 50 = 259 200 (пикселов).
ЗамечаниеЕсли кому-то эти рассуждения не очень понятны, давайте эту формулу запишем еще проще. По длине каждый дюйм состоит из 72 пикселов, следовательно, длина включает 72 х 10 = 720 (пикселов). По ширине каждый дюйм также состоит из 72 пикселов, следовательно, ширина включает 72 х 5 = 360 (пикселов). Количество пикселов во всем изображении будет равно произведению этих величин: 720 х 360 = 259 200 (пикселов). Удивительно, но получилось одно и то же число пикселов.
Запишем эти действия в одну строку:
(72 х 10) х (72 х 5) = 72 х 72 х 5 х 10 = 722 х 5 х 10 = 259 200.
samoychiteli.ru
Решение задач по теме «Количество информации»
Возможны следующие сочетания известных (Дано) и искомых (Найти) величин:
Если к этим задачам добавить задачи на соотношение величин, записанных в разных единицах измерения, с использованием представления величин в виде степеней двойки мы получим 9 типов задач. Рассмотрим задачи на все типы. Договоримся, что при переходе от одних единиц измерения информации к другим будем строить цепочку значений. Тогда уменьшается вероятность вычислительной ошибки.Задача 1. Получено сообщение, информационный объем которого равен 32 битам. чему равен этот объем в байтах?
Решение: В одном байте 8 бит. 32:8=4 Ответ: 4 байта.
Задача 2. Объем информацинного сообщения 12582912 битов выразить в килобайтах и мегабайтах.
Решение: Поскольку 1Кбайт=1024 байт=1024*8 бит, то 12582912:(1024*8)=1536 Кбайт и поскольку 1Мбайт=1024 Кбайт, то 1536:1024=1,5 Мбайт Ответ:1536Кбайт и 1,5Мбайт.
Задача 3. Компьютер имеет оперативную память 512 Мб. Количество соответствующих этой величине бит больше:
1) 10 000 000 000бит 2) 8 000 000 000бит 3) 6 000 000 000бит 4) 4 000 000 000бит Решение: 512*1024*1024*8 бит=4294967296 бит. Ответ: 4.Задача 4. Определить количество битов в двух мегабайтах, используя для чисел только степени 2. Решение: Поскольку 1байт=8битам=23битам, а 1Мбайт=210Кбайт=220байт=223бит. Отсюда, 2Мбайт=224бит. Ответ: 224бит.
Задача 5. Сколько мегабайт информации содержит сообщение объемом 223бит? Решение: Поскольку 1байт=8битам=23битам, то 223бит=223*223*23бит=210210байт=210Кбайт=1Мбайт. Ответ: 1Мбайт
Задача 6. Один символ алфавита "весит" 4 бита. Сколько символов в этом алфавите? Решение: Дано:
| i=4 | По формуле N=2i находим N=24, N=16 |
| Найти: N - ? |
Задача 7. Каждый символ алфавита записан с помощью 8 цифр двоичного кода. Сколько символов в этом алфавите? Решение: Дано:
| i=8 | По формуле N=2i находим N=28, N=256 |
| Найти:N - ? |
Задача 8. Алфавит русского языка иногда оценивают в 32 буквы. Каков информационный вес одной буквы такого сокращенного русского алфавита? Решение: Дано:
| N=32 | По формуле N=2i находим 32=2i, 25=2i,i=5 |
| Найти: i- ? |
Задача 9. Алфавит состоит из 100 символов. Какое количество информации несет один символ этого алфавита? Решение: Дано:
| N=100 | По формуле N=2i находим 32=2i, 25=2i,i=5 |
| Найти: i- ? |
Задача 10. У племени "чичевоков" в алфавите 24 буквы и 8 цифр. Знаков препинания и арифметических знаков нет. Какое минимальное количество двоичных разрядов им необходимо для кодирования всех символов? Учтите, что слова надо отделять друг от друга! Решение: Дано:
| N=24+8=32 | По формуле N=2i находим 32=2i, 25=2i,i=5 |
| Найти: i- ? |
Задача 11. Книга, набранная с помощью компьютера, содержит 150 страниц. На каждой странице — 40 строк, в каждой строке — 60 символов. Каков объем информации в книге? Ответ дайте в килобайтах и мегабайтах Решение: Дано:
| K=360000 | Определим количество символов в книге 150*40*60=360000. Один символ занимает один байт. По формуле I=K*iнаходим I=360000байт 360000:1024=351Кбайт=0,4Мбайт |
| Найти: I- ? |
Задача 12. Информационный объем текста книги, набранной на компьютере с использованием кодировки Unicode, — 128 килобайт. Определить количество символов в тексте книги. Решение: Дано:
| I=128Кбайт,i=2байт | В кодировке Unicode один символ занимает 2 байта. Из формулыI=K*i выразимK=I/i,K=128*1024:2=65536 |
| Найти: K- ? |
Задача 13.Информационное сообщение объемом 1,5 Кб содержит 3072 символа. Определить информационный вес одного символа использованного алфавита Решение: Дано:
| I=1,5Кбайт,K=3072 | Из формулы I=K*i выразимi=I/K,i=1,5*1024*8:3072=4 |
| Найти: i- ? |
Задача 14.Сообщение, записанное буквами из 64-символьного алфавита, содержит 20 символов. Какой объем информации оно несет? Решение: Дано:
| N=64, K=20 | По формуле N=2i находим 64=2i, 26=2i,i=6. По формуле I=K*i I=20*6=120 |
| Найти: I- ? |
Задача 15. Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если его объем составил 1/16 часть мегабайта? Решение: Дано:
| N=16, I=1/16 Мбайт | По формуле N=2i находим 16=2i, 24=2i,i=4. Из формулы I=K*i выразим K=I/i, K=(1/16)*1024*1024*8/4=131072 |
| Найти: K- ? |
Задача 16. Объем сообщения, содержащего 2048 символов,составил 1/512 часть мегабайта. Каков размер алфавита, с помощью которого записано сообщение? Решение: Дано:
| K=2048,I=1/512 Мбайт | Из формулы I=K*i выразим i=I/K, i=(1/512)*1024*1024*8/2048=8. По формулеN=2iнаходим N=28=256 |
| Найти: N- ? |
- Каждый символ алфавита записывается с помощью 4 цифр двоичного кода. Сколько символов в этом алфавите?
- Алфавит для записи сообщений состоит из 32 символов, каков информационный вес одного символа? Не забудьте указать единицу измерения.
- Информационный объем текста, набранного на компьюте¬ре с использованием кодировки Unicode (каждый символ кодируется 16 битами), — 4 Кб. Определить количество символов в тексте.
- Объем информационного сообщения составляет 8192 бита. Выразить его в килобайтах.
- Сколько бит информации содержит сообщение объемом 4 Мб? Ответ дать в степенях 2.
- Сообщение, записанное буквами из 256-символьного ал¬фавита, содержит 256 символов. Какой объем информации оно несет в килобайтах?
- Сколько существует различных звуковых сигналов, состоящих из последовательностей коротких и длинных звонков. Длина каждого сигнала — 6 звонков.
- Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 20 до 100%, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите информационный объем результатом наблюдений.
- Скорость передачи данных через ADSL-соединение равна 512000 бит/с. Через данное соединение передают файл размером 1500 Кб. Определите время передачи файла в секундах.
- Определите скорость работы модема, если за 256 с он может передать растровое изображение размером 640х480 пикселей. На каждый пиксель приходится 3 байта. А если в палитре 16 миллионов цветов?
1811-info.ru
- Битрикс curl
- Команды убунту терминал
- Команды html для сайта

- Как установить windows 10 с нуля
- Подстановка данных из excel в word

- Как чистить системный блок

- Специалист в сфере информационных технологий

- Папка это файл

- Эта программа заблокирована в целях защиты windows 7

- Xp не загружается

- Как выкрутить гамму на windows 10

