30.1. СЕТЕВЫЕ МОДЕЛИ. Основные понятия сетевой модели. Статические сетевые модели
Сетевые информационные модели
Сетевые информационные модели применяются для сложных систем, в которых связи между элементами имеют произвольный характер.
Например, различные региональные части глобальной компьютерной сети Интернет (американская, европейская, российская, австралийская и так далее) связаны между собой высокоскоростными линиями связи. При этом, одни части, например, американская, имеют прямые связи со всеми региональными частями только через американскую часть Интернета, а другие, например, российская и австралийская, могут обмениваться информацией между собой.
Впрочем, любые компьютерные сети глобальные или локальные имеют сетевую структуру.
Например, на рис. 3.10 представлен граф, отражающий структуру локальной сети из пяти компьютеров.

Как видно из рисунка, граф показывает не только расположение Персональных Компьютеров в сети, но и их соединение друг с другом. Сервер (ПК №1) связан односторонней связью со всеми ПК в сети и управляет их работой. Односторонняя связь свидетельствует о том, что Сервер имеет доступ к информационным ресурсам всех компьютеров сети, а ПК2, ПК3, ПК4 и ПК5 доступа к Серверу не имеют. Однако, ПК2, ПК3, ПК4 и ПК5 имеют двустороннюю связь между собой. Это означает, что они имеют доступ друг к другу и могут обмениваться информационными ресурсами.
Представленная сетевая информационная модель является статической моделью. С помощью сетевой динамической модели можно, например, описать процесс передачи мяча между игроками в коллективной игре (футболе, баскетболе и так далее).
3.11 Контрольные вопросы
1. Что такое информационная модель?
2. По каким признакам можно классифицировать модели?
3. Какие системы объектов целесообразно и возможно представлять с помощью сетевых моделей?
4. Перечислите этапы построения информационных моделей.
5. Что такое агрегирование и декомпозиция?
6. Приведите пример компьютерных информационных моделей.
7. Для чего нужны компьютерные эксперименты?
8. Чем отличается табличная структура информационной модели от иерархической?
9. Что такое граф. Что отображается при помощи графа?
10. Могут ли элементы одного уровня иерархической структуры быть связаны друг с другом?
Методы моделирования
Получение моделей в общем случае – процедура неформализованная. Основные решения, касающиеся выбора вида математических соотношений, характера используемых переменных и параметров, принимает проектировщик. В тоже время такие операции, как расчет численных значений параметров модели, определение областей адекватности и другие, алгоритмизированы и решаются на ЭВМ. Поэтому моделирование элементов проектируемой системы обычно выполняется специалистами конкретных технических областей с помощью традиционных экспериментальных исследований.
Все методы получения функциональных моделей элементов делят на теоретические и экспериментальные.
Теоретические методы основаны на изучении физических закономерностей протекающих в объекте процессов, определении соответствующего этим закономерностям математического описания, обосновании и принятии упрощающих предположений, выполнении необходимых выкладок и приведении результата к принятой форме представления модели.
Экспериментальные методы основаны на использовании внешних проявлений свойств объекта, фиксируемых во время эксплуатации однотипных объектов или при проведении целенаправленных экспериментов.
Основой выбора методов моделирования является классификация. Систематизация известных к настоящему времени моделей и методов их использования позволяет утверждать о правомерности классификации, изображенной на схеме [22]
| Рис. 4.1 Классификация методов моделирования |

Как видно на схеме все методы моделирования делятся на две группы: материальное моделирование, в которое объединены экспериментальные методы и идеальное моделирование, объединяющее все теоретические методы.
poisk-ru.ru
Статические и динамические модели — Мегаобучалка
Статическойназывается модель объекта, отражающая оригинал в какой-то отдельный момент времени, т.е. «моментальная фотография» объекта. Например, буквально фотография или схема.
С фотографией (рис. 1.11) все ясно, что же касается схемы, то даже если это структурная схема с указанием передаточных функций звеньев, по ней явно не видно, как модель изменяется с течением времени (рис. 1.12).
Рис.1.11. Фотография как пример статической модели
Рис. 1.12. Структурная схема системы
Другой очевидный и знакомый пример статической модели –статическая характеристика, т.е. зависимость выходной переменной объекта (системы) от входной переменной в установившемся режиме, т.е. при t®∞: y(∞)=F[x(∞)] (рис. 1.13).
Рис. 1.13. Статическая характеристика системы ”System”
Динамическаямодель, в отличие от статической, учитывает изменения, происходящие в системе с течением времени. Это может выражаться в зависимости входной, выходной и промежуточных переменных от времени. Примером могут служить переходные функции – реакции систем на единичное ступенчатое входное воздействие (рис. 1.14).
Рис. 1.14. Переходная функция h(t) системы “System”
Обычно переходные функции получаются в результате: 1) аналитического решения; 2) численного интегрирования дифференциальных уравнений, описывающих исследуемую систему; 3) обратного преобразования Лапласа от передаточной функции системы, деленной на s. Модельв виде дифференциальных уравнений (ДУ) является широко распространенной динамической моделью.
Пример. Пусть система описывается моделью в виде дифференциального уравнения:
входное воздействие x(t)=1[t] – единичное ступенчатое (как на рис. 1.14), а начальные условия имеют вид: y(t=0) = 0, т.е. процесс начинается из начала координат.
Аналитическое решение. Это линейное дифференциальное уравнение первого порядка с постоянными коэффициентами (стационарное). Его решение складывается из двух слагаемых – общего и частного решения:
Общее решение ищется в виде:
где А – неизвестный коэффициент, определяемый из начальных условий;
l – корень характеристического уравнения, которое в данном случае выглядит так:
,
откуда l=–2.
В стандартной форме исходное уравнение должно иметь при y(t) коэффициент, равный единице. Для этого исходное уравнение разделим на 4 и получим:
Частное решение зависит от вида правой части ДУ; в данном примере, поскольку x(t)=1[t], частное решение будет равно константе:
Суммарное решение будет выглядеть так:
Теперь, подставив в решение y(t) начальное условие (для уравнения 1-го порядка оно одно), можно найти значение коэффициента А:
откуда А = –1,25. Окончательно решение имеет вид:
Поскольку входным воздействием было единичное ступенчатое, то полученное решение является переходной функцией и обозначается, как обычно, h(t). График этой функции показан на рис. 1.15.

Рис. 1.15. Переходная функция h(t) – решение ДУ из примера
Подобный h(t) характер (с разной погрешностью) имеют такие процессы, как разгон автомобиля, нагрев жидкости, накопление знаний в некоторой предметной области, увеличение численности популяции животных, рост производства (при определенных условиях) и многие другие. В этом заключается одно из важнейших свойств математическихмоделей – их универсальность.
megaobuchalka.ru
Сетевая модель и ее основные элементы. Правила построения сетевых моделей.
Модели сетевого планирования и управления (модели СПУ) предназначены для планирования и управления сложными комплексами работ (проектами), направленными на достижение определенной цели в заданные сроки (строительство, разработка и производство сложных объектов и др.).
За рубежом система СПУ известна как система PERT (Program
Evaluation and Review Technique – метод анализа и оценки программ) или CPM (Critical Path Method – метод критического пути).
Сетевой моделью (СМ) называется экономико-математическая модель,
отражающая весь комплекс работ и событий, связанных с реализацией проекта в их логической и технологической последовательности и связи. Математическим аппаратом СМ является теория графов.
Графом называется совокупность двух конечных множеств: множества
точек (х1, х2, …, xn), которые называются вершинами, и множества пар вершин, которые называются ребрами (e1, e2, …, en). Если пары вершин упорядочены, т.е. на каждом ребре задано направление, ребро называется дугой, а граф называется ориентированным; иначе – неориентированным. Последова- тельность ребер, ведущая от некоторой вершины к другой вершине, образует путь. Замкнутый путь называется циклом. Граф называется связным, если для любых двух вершин существует путь, их соединяющий. В противном случае граф называется несвязным. Если дугам (i, j) присвоены некоторые числа или веса (Cij), то граф называется нагруженным. В ориентированном графе вершины, не имеющие входных дуг, называются начальными (источниками), а вершины, не имеющие выходных дуг – конечными (стоками), остальные – промежуточными.
В СПУ применяются связные, ориентированные графы без циклов,
имеющие одну начальную и одну конечную вершину.
Основные понятия сетевой модели : событие, работа, путь.
Работа характеризует любое действие, требующее затрат времени или ресурсов. Работами считаются и процессы, не требующие затрат времени и
ресурсов, а устанавливающие зависимости выполнения работ. Такие работы называются фиктивными. Работа обозначается парой чисел (i, j), где i – номер события, являющимся начальным для данной работы, j – номер события, являющимся конечным для данной работы, в которое она входит. Работа не может начаться раньше, чем свершится событие, являющееся для нее
начальным. Каждая работа имеет свою продолжительность t(i, j). Работы на графах обозначаются дугами (стрелками), фиктивные работы обозначаются пунктирными стрелками.
Событиями называются начало или завершение одной или нескольких работ. Они не имеют протяженности во времени. Событие совершается в тот момент, когда оканчивается последняя работа, входящая в него. На графе события изображаются кружками, внутри которых записывается номер события. В моделях СПУ имеется одно начальное событие (номер 0), одно конечное событие или завершающее (номер N) и промежуточные события (номер i). В графической интерпретации сетевой модели работы представляются дугами, а события – вершинами графа.
Путь – цепочка следующих друг за другом работ (дуг), соединяющих начальную и конечную его вершины. Полный путь L – путь, начало которого
совпадает с начальным событием сети, а конец – с завершающим.
Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную продолжительность,
называют критическим (обозначение Lкр). Продолжительность критического пути обозначается как tкр.. Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ.
Сетевая модель должна удовлетворяет следующим требованиям:
1. Не должно быть событий с одинаковыми номерами.
2. Для каждой работы (i, j) должно выполняться i < j.
3. Должны быть только одно начальное и одно конечное события.
4. Должны отсутствовать циклы, т.е. замкнутые пути, соединяющие событие с ним же самим.
При выполнении этих требований можно приступать к вычислениям числовых характеристик СМ. Исходные числовые данные СМ представляются
в виде таблицы длительности выполнения каждой работы.
studfiles.net
Характеристики элементов сетевой модели
При расчетах для сетевой модели определяются следующие характеристики ее элементов.
Характеристики событий
1. Ранний срок свершения события tp(0) = 0, tp(j) = maxi{tp(i) + t(ij)}, j = 1 – N характеризует самый ранний срок завершения всех путей, в него входящих. Этот показатель определяется «прямым ходом» по графу модели, начиная с начального события сети.
2. Поздний срок свершения события tп(N) = tp(N), tп(i) = minj{tп(j) – t(ij)}, i = 1 – (N – 1) характеризует самый поздний срок, после которого остается ровно столько времени, сколько требуется для завершения всех путей, следующих за этим событием. Этот показатель определяется «обратным ходом» по графу модели, начиная с завершающего события сети.
3. Резерв времени события R(i) = tп(i) – tp(i) показывает, на какой максимальный срок можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения всего комплекса работ.
Резервы времени для событий на критическом пути равны нулю, R(i) = 0.
Характеристики работы (I, j)
1.Ранний срок начала работы: tpн(i,j) = tp(i).
2.Ранний срок окончания работы: tpo(i,j) = tpн(i,j) + tij = tp(i) + tij.
3. Поздний срок начала работы: tпн(i,j) = tп(j) – tij.
4. Поздний срок окончания работы: tпо(i,j) = tп(j).
5. Резервы времени работ:
•полный резерв Rп(i, j) = tп(j) – tp(i) – tij –
максимальный запас времени, на который можно отсрочить начало или
увеличить длительность работы без увеличения длительности критического пути. Работы на критическом пути не имеют полного резерва времени, для них Rп(i, j) = 0;
•частный резерв R1(i,j) = Rп(i,j) – R(i) = tп(j) – tп(i)– tij –
часть полного резерва, на которую можно увеличить продолжительность
работы, не изменив позднего срока ее начального события;
•свободный резерв Rс(i,j) = Rп(i,j) – R(j) = tp(j) – tp(i) – tij –
максимальныйзапасвремени, накоторыйможнозадержатьначалоработыили
(если она началась в ранний срок) увеличит ее продолжительность, не изменяя ранних сроков начала последующих работ;
•независимый резерв Rн(i,j)= Rп(i,j) – R(i) – R(j) = tp(j) – tп(i) – tij –
запасвремени, при котором все предшествующие работы заканчиваются в
поздние сроки, а все последующие – начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени других работ.
Сделаем ряд замечаний. Работы, лежащие на критическом пути, резервов времени не имеют. Если на критическом пути Lкр лежит начальное событие i работы (i, j), то Rп(i, j) = R1(i, j). Если на Lкр лежит конечное событие j работы (i, j), то Rп(i, j) = Rc(i, j). Если на Lкр лежат и событие i, и событие j работы (i, j), а сама работа не принадлежит критическому пути, то Rп(i, j) = Rс(i, j) = Rн(i, j).
Характеристики путей
1. Продолжительность пути равна сумме продолжительностей составляющих ее работ.
2. Резерв времени пути равен разности между длинами критического
пути и рассматриваемого пути.
Резерв времени пути показывает, на сколько может увеличиться продолжительность работ, составляющих данный путь, без изменения
продолжительности срока выполнения всех работ.
В сетевой модели можно выделить так называемый критический путь. Критический путь Lкр состоит из работ (i, j), у которых полный резерв времени равен нулю Rп(i, j) = 0, кроме этого, резерв времени R(i) всех событий i на критическом равен 0. Длина критического пути определяет величину наиболее длинного пути от начального до конечного события сети и равнаtкр = tp(N) = tп(N). Заметим, что в проекте может быть несколько критических путей.
),
3. Коэффициент напряженности работ
Видно, что Кн(i, j) < 1. Чем ближе Кн(i, j) к 1, тем сложнее выполнить данную работу в установленный срок. Напряженность критических работ полагается равной 1. Все работы сетевой модели могут быть разделены на 3 группы: напряженные (Кн(i, j) > 0,8), надкритические (0,6 < Кн(i, j) < 0,8) и резервные (Кн(i, j) < 0,6).
В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ, что возможно при переводе всех работ в первую группу.
studfiles.net
СТАТИЧЕСКИЕ МОДЕЛИ ОПТИМАЛЬНОГО - Энциклопедия по экономике
СТАТИЧЕСКИЕ МОДЕЛИ ОПТИМАЛЬНОГО ОБНОВЛЕНИЯ ТЕХНИКИ [c.5]Из данного примера видно, что нахождение размера удельных приведенных затрат производства продукции на новой технике и ее оптимального срока службы по формуле (5.18) полностью соответствует принципу нахождения оптимального момента замены техники, установленному в гл. 1 на основе рассмотрения статических моделей оптимального плана. [c.125]
Решение этой задачи дает оптимальную структуру территориального распределения предприятий при заранее заданном спросе. Такая структура может быть достигнута отраслью через некоторое время в результате строительства новых мощностей. Сам процесс этого строительства и выпуск продукции отраслью в процессе перестройки в сформулированной здесь модели не описываются. К более сложной модели, описывающей процесс перестройки, можно перейти так же, как это делалось в главе, посвященной балансовым моделям экономики, когда осуществлялся переход от статической модели к динамической. При этом придется отдельно рассматривать затраты на строительство и текущие затраты производства. Мы не будем здесь формулировать модель перестройки отрасли. Вместо этого рассмотрим некоторые достоинства и недостатки нашей модели и попытаемся указать способы устранения этих недостатков. [c.171]До сих пор мы рассматривали методы решения задач оптимизации для статических моделей. Дадим краткую характеристику методов решения динамических задач оптимизации (или, как принято говорить, задач оптимального управления). [c.58]
Только здесь переменные модели являются функциями времени. Если модель является многошаговой (например, типа (3.18), (3.21) — (3.23)), то в случае конечного числа шагов каждая функция времени описывается конечным числом скалярных величин, так что задачу оптимального управления удается свести к некоторой задаче оптимизации для специально сконструированной статической модели. Для ее решения можно применить упоминавшиеся ранее методы оптимизации. В частности, если динамическая модель является линейной, т. е. удовлетворяет соотношениям (3.18), (3.19), (3.23), (3.24), то можно применить методы линейного программирования. При этом задача линейного программирования благодаря своему происхождению имеет специальную форму, которой можно воспользоваться для упрощения расчетов. [c.58]
В середине 1960 гг. в ЦЭМИ АН СССР в результате обобщения и дальнейшего развития идей, изложенных в работах [2,3], была разработана методика оптимального текущего планирования нефтеперерабатывающих предприятий [5, 6]. В частности, в работе [5] сформирована линейная статическая модель с фиксированным набором технологических режимов и способов смешения. Кроме того, рассматриваются статическая модель с переходящими запасами и динамическая модель с блочной структурой. [c.14]
Таким образом, динамическая модель модифицируется в так называемую последовательность статических моделей, в которой оптимальный вариант развития и размещения системы нефтеснабжения определяется путем поэтапного расчета статических моделей. При использовании таких подходов учета динамики в задачах перспективного развития и размещения нефтебазового хозяйства встает вопрос увязки, условно-оптимальных планов статических задач. На наш взгляд, представляет интерес алгоритм увязки статических решений, разработанный, в Сибирском энергетическом институте (СЭИ) СО АН СССР, который базируется на методах блочного программирования. [c.75]
Статические модели, входящие в единую динамическую модель, отличаются одна от другой по степени детализации и учета различных факторов, влияющих на формирование оптимального плана развития и размещения нефтебазового хозяйства на различных этапах планового периода. [c.76]
Статические модели поиска оптимальной структуры как раз и пред- [c.58]
Статическая модель оптимизации прикрепления потребителей к поставщикам. Основной математической моделью оптимального прикрепления потребителей к поставщикам является так называемая транспортная задача линейного программирования, которая в общем виде формулируется следующим образом [c.524]
Для выявления и обоснования принципов оптимального обновления техники в данной главе рассмотрена серия статических многопродуктовых моделей оптимального плана, в которых ставится задача минимизировать предстоящие текущие затраты производства заданного планом в ассортименте и объеме продукта при установленных ресурсных ограничениях и ограничениях, обеспечивающих выполнение плановых заданий . [c.5]
Вновь созданная лучшая техника обеспечивает максимальную экономию предстоящих текущих затрат по сравнению с текущими издержками на замыкающей технике и, соответственно, при продаже продукта по цене равной его оценке в оптимальном плане, обеспечивает максимальную разницу между текущими доходами от реализации продукта и текущими расходами на его производство. За счет этого в первый период использования новой техники выявляется максимальная возможность возмещения через амортизацию затрат в создание этой техники и получение прибыли. (Так как в данной главе исследуются статические модели, то здесь не рассматривается вопрос учета относительно высокого уровня затрат производства продукции в период освоения новой техники. Этот вопрос будет рассмотрен при исследовании процесса изменения затрат на производство продукции во времени.) [c.47]
Практически применяемыми и наиболее разработанными являются статические модели, использующие минимум приведенных затрат в качестве критерия оптимальности. Оптимальный план, разрабатываемый с помощью таких моделей, позволяет обеспечить решение следующих задач выбор вариантов реконструкции и расширения действующих предприятий, определение мест строительства новых заводов, расчет специализации и оптимальных размеров вновь строящихся и реконструируемых предприятий, опреде ление действующих производств, предназначенных к ликвидации. Более совершенны в методическом отношении динамические модели, в которых минимизируются затраты за период на основе применения интегральных показателей. [c.259]
Такого рода модели учитывают динамику развития экономической системы. И если, как отмечалось, статический межотраслевой баланс — это моментальная фотография, то динамические модели межотраслевого баланса можно считать чем-то в роде документального кинофильма. Но ни те, ни другие модели не могут полностью решить главной задачи экономической динамики — рассчитать оптимальные темпы и пропорции развития отраслей народного хозяйства. Прогресс в решении этой задачи будет, вероятно, достигнут на других путях. Мы имеем в виду, прежде всего, интенсивно разрабатываемую сейчас теорию динамических моделей оптимального планирования. [c.155]
Следует отметить наряду с общеметодологическими трудностями и специфические особенности в вопросе выбора крите рия оптимальности для отдельных типов моделей. Так, в статической модели можно сравнительно просто описать структуру конечного продукта в части предметов потребления, но гораздо сложнее учесть средства производства, идущие на капиталовложения, поскольку они предназначены для будущих периодов и их состав определяется в зависимости от планов будущих лет. Решение последней проблемы в известной мере облегчается при переходе к динамической модели. Однако в ней выбор критерия оптимальности является сложной задачей. Здесь он должен включать оптимальные пропорции разделения национального дохода на потребление и накопление, оптимальные темпы роста производственного и личного потребления и др. Критерий оптимальности должен учитывать также состояние и потенциальные возможности экономической системы на конец планового периода. [c.178]
Указанные модели носят статический характер, т. е. решаются для строго определенного периода, и не учитывают динамики производства. Оптимальный вариант с учетом развития предприятия можно найти на основе динамического программирования, которое, однако, еще недостаточно разработано. [c.128]
При большом числе плановых задач по определению оптимального способа организации работ и использования оборудования применяют имитационные модели, воспроизводящие экономические и производственные условия с помощью ЭВМ. Из методов статического моделирования применяют метод Монте-Карло, сетевые модели и др. [c.128]
Для оптимизации производственной программы разработан ряд статических экономико-математических моделей, основанных на методах линейного программирования и с достаточной точностью описывающих возможности нефтеперерабатывающего предприятия. Критериями оптимальности служат максимум прибыли, минимум затрат, максимум выработки товарной про- [c.162]
Дальнейшее развитие и использование экономико-математических моделей должно идти по линии их совершенствования, перехода от статических задач к динамическим, Совершенствования критериев выбора оптимальных хозяйственных решений, уточнения методики разработки исходных нормативов. [c.168]
На практике возникает большое количество плановых задач, где необходимо определить оптимальный способ организации работ и использования оборудования. В этом случае используется статическое моделирование, заключающееся в имитации экономических и производственных условий на ЭВМ путем воспроизведения элементарных явлений и актов процесса, в последовательности, отражающей реальные связи и взаимозависимости. Из методов статического моделирования используется метод Монте-Карло, сетевые модели. Содержание, назначение и методика составления последнего рассматриваются в главе XII, 3. [c.89]
Первые два направления могут обеспечить некоторое количественное уточнение оптимальной кратности запасов газа. Наиболее же перспективно третье направление, которое, однако, могут ограничить вычислительные возможности методов стохастического программирования. Дело в том, что задача учета в модели нескольких адаптивных характеристик в некоторых случаях реализуема только при статической постановке. [c.75]
Учет динамического характера задачи оптимального развития и размещения нефтебазового хозяйства можно осуществлять не только решением ряда статических задач на серию взаимосвязанных периодов, но и решением единой задачи, ограничения которой построены с разбивкой по временным отрезкам планового периода. Единая динамическая модель для всего планового периода может охватывать 10—15 лет и более. Единый критерий оптимальности обеспечивает непротиворечивость решений для отдельных этапов планового периода. [c.76]
Третий блок единой динамической модели отражает условия формирования статической задачи по данным 1990 г. Модель включает в себя четыре этапа. Однако в ней не отражено деление года на сезоны и отсутствует деление на виды нефтепродуктов. По потребителям задаются ограничения, соответствующие общему объему светлых нефтепродуктов. За критерий оптимальности принимается минимум суммарных текущих и ка питальных затрат. Для описания модели введем ряд обозначений. [c.92]
С помощью статической М.и. можно выявить, при каких сочетаниях экзогенных (вводимых) факторов достигается оптимальный результат изучаемого процесса, установить относительное значение тех или иных факторов. Это полезно, напр., при изучении различных методов и средств экономического стимулирования на производстве. М.и. в форме "проигрывания" динамических моделей (динамической М.и.) применяется также в прогнозировании. С его помощью изучают возможные последствия крупных структурных сдвигов в экономике, внедрения важнейших научно-технических достижений, принятия плановых решений. [c.190]
В качестве критерия оптимальности в большинстве отраслевых задач выступает минимум затрат на заданный объем конечного продукта рассматриваемой производственной системы. Применяются экономико-математические модели разных типов динамические и статические, детерминированные и вероятностные, однопродуктовые и многопродуктовые, с дискретными и непрерывными переменными, производственные функции, производственно-транспортные задачи и, наконец, по характеру отображения хозяйственных связей —матричные и сетевые модели. [c.253]
Хотя модель Курно является статической игрой, рассмотрим следующую ее динамическую интерпретацию. В первом периоде Фирма 1 выбирает определенный объем производства. После этого во втором периоде Фирма 2 выбирает оптимальный объем производства в зависимости от выбора Фирмы 1. Далее, в третьем периоде снова черед Фирмы 1 выбирать оптимальный объем производства, учитывая текущий объем производства Фирмы 2, и т.д. Фирма 1 выбирает объем производства в нечетных периодах, Фирма 2 — в четных. [c.128]
В предыдущих главах мы познакомились с задачами управления в организационных системах, точнее — с задачами построения оптимальных организационных механизмов. При этом структура организационной системы предполагалась двухуровневой (центр и подчиненные ему элементы), а модель ограничений — детерминированной и статической. Рассматривались случай полной информированности центра, а также случай применения встречного способа формирования данных в условиях неполной информированности. Наряду с рассмотренными практический интерес представляет еще ряд схем функционирования двухуровневых организационных систем. Здесь можно назвать системы с использованием процедуры формирования данных с памятью, адаптивные схемы управления, итерационные схемы планирования. Дополнительные проблемы возникают при расширении рассмотренных моделей. Дело в том, что реальные организации, как правило, имеют многоуровневую структуру, их модели ограничений включают случайные и неопределенные факторы, а функционирование носит динамический характер. В связи с этим возникают три проблемы. Первая носит методологический характер и связана с обобщениями введенных понятий и постановок задач. Вторая связана с вопросом, насколько результаты, полученные для двухуровневых статических детерминированных систем, переносятся на более сложные случаи. Третья проблема — исследование эффектов, не имеющих аналогов в более простых системах. Обсуждение этих проблем и проводится в данной главе. [c.286]
Приведем один из упрощенных вариантов статической союзной модели комплексной оптимальной химизации сельского хозяйства. [c.359]
Модель статическая, т. е. не показывает изменение производства во времени. Вместе с тем структура модели проста и логически увязана с моделью расчета оптимальной производственной программы нефтеперерабатывающих предприятий. Планирующий орган (Миннефтехимпром) на основе заводских планов разрабатывает оптимальный план отрасли и сообщает предприятиям новые задания по объемам поставки нефтей, продукции и оценок ограниченных ресурсов. [c.170]
К.— один из основателей экономико-математич. направления в СССР. Впервые построил оптимальную статическую и динамич. модели текущего и перспективного планирования разработал принципиально но-ный метод построения системы экономич. показателей. В работах К. модели оптимизации использованы при исследовании вопросов ценообразования, эффективности капитальных вложений, теории ренты, теории амортизации и др. проблем социалистической экономики. Гос. пр. СССР (1949), Ленинская пр. (1965). Иностранный член зарубежных академий (США, Венгрия). [c.96]
При таком анализе всегда рассматривается комплекс линейных оптимизационных моделей. Это придает модели определенную Динамичность, позволяющую исследователю проанализировать влияние возможных изменений исходных условий на полученное ранее оптимальное решение. Динамические характеристики моделей фактически отображают аналогичные характеристики, свойственные реальным процессам. Отсутствие методов, позволяющих выявлять влияние возможных изменений параметров модели на оптимальное решение, может привести к тому, что полученное (статическое) решение устареет еще до своей реализации. Для проведения анали- [c.208]
Таким образом, даже для модели идеализированной экономики оценки оптимального плана представляют определенную ценность. И это следствие того, что модель— не условная схема, а отражение определенных реальных условий. Отсюда становится понятным, почему анализ статической и динамической линейно-программных моделей позволяет сделать ряд общих выводов о структуре цен, характеристике оптимального плана, эффективности капиталовложений, которые имеют значение даже для тех случаев, когда не полностью выполнены гипотезы, лежащие в основе этих моделей. Эти общие выводы имеют поэтому гораздо более широкую область применения. [c.170]
Статьи [20 - 22] касаются статических задач выбора портфеля при целевой функции в виде линейной комбинации среднего и дисперсии. В [20] показывается, что ошибки в оценке среднего значения оказывают решающее воздействие на точность формирования портфеля. При этом погрешности в оценке средних оказываются приблизительно в десять раз более существеннее, чем погрешности в оценке дисперсии. В [21] проводится дальнейшее изучение этой темы, рассматриваются способы отбора входной и выходной информации с целью получения лучших инвестиционных решений. В [22] разработана модель, которая позволяет проследить по истечении некоторого времени за воздействием различных источников на "результат работы" данного портфеля. А именно, капитал распределяется между разными портфелями ранее предполагавшихся оптимальными, портфелями, интуитивно предпочитаемыми экспертами - менедже- [c.8]
Влияние регионального фактора при решении вопроса обновления техники рассматривается здесь с помощью многопродуктовой статической модели оптимального плана, развивающей модель раздела 1.2. В этой модели минимизируются предстоящие текущие затраты на производство заданного по объему и ассортименту продукта. Помимо ресурса капитальных вложений в создание новой техники и ресурса ранее созданной неремонтируемой техники в ней учитывается ограниченность ресурса относительно пучшего местоположения для вьшуска продукции. [c.22]
В первой главе с помощью статических моделей оптимального плана было обосновано условие целесообразности проведения капитального ремонта капитальный ремонт экономически целесообразно осуществлять, если удельные приведенные затраты после ремонта (ПЗПР) не превышают удельных приведенных затрат производства продукции на новой технике [ формула (1.6)]. [c.129]
Математические модели, кроме того, подразделяют на равновесные, которые описывают равновесие, поэтому их можно назвать описательными (дискриптивными), и модели оптимизации, которые позволяют установить оптимальные, т.е. наилучшие по какому-то определенному критерию, параметры системы Выделяют статические модели, описывающие состояние объекта в конкретный момент или период времени, и динамические модели, включающие взаимосвязи переменных во времени. [c.15]
В статических моделях было условно принято, что в приведенных за-претах заранее известен размер амортизационных отчислений на реновацию и капитальный ремонт. Но уже исследование статических" моделей показало, что действующий механизм равномерной амортизации не отражает тенденции износа техники в оптимальном плане. Подробно механизм формирования амортизационных отчислений на реновацию с учетом тенденций износа техники будет рассмотрен в следующей главе. Но проведенные выше исследования учета фактора времени в оптимальном плане позволяют предложить еще один подход к обоснованию целесообразности проведения капитального ремонта. [c.129]
Как было показано еще в гл. 1 на статических моделях, оценка ОП техники (ее прокатная оценка), равная экономии от использования этой относительно лучшей техники по сравнению с замыкающей техникой в данной сфере производства, является источником формирования амортизации и нормативного эффекта капитальных вложений (основы платы за фонды). Причем было показано, что плата за фонды должна взиматься с остаточной стоимости ОПФ на уровне норматива эффективности капитальных вложений. Именно на этой посылке в разделе 5.1 обосновывается необходимость приведения затрат во времени по сложным процентам на базе норматива эффективности капитальных вложений. Поэтому снижающуюся плату за фонды, предложенную В. Н. Лившицем, следует разделить на собственно плату за фонды на уровне норматива эффективности капитальных вложений с остаточной стоимости ОПФ и собственно амортизацию. При этом перенос стоимости на продукт с целью простого воспроизводства стоимости будет осуществляться через амортизацию, а нормативный эффект остаточной стоимости при ценах на уровне цен оптимального плана будет выступать как часть вновь созданной стоимости, не учитываемая в издержках производства. Причем если в себестоимости учтены все эатра- [c.158]
Наиболее богатый опыт оптимального планирования экономики накоплен в отраслевом планировании. По решению Госплана СССР оптимальные планы составлялись в последние годы более чем по 70 отраслям, охватывающим более половины промышленной продукции. Они использовались при составлении пятилетних планов. Для решения текущих задач функционирования и развития отрасли довольно широко применяются статические модели, связанные с использованием наличных производственных мощностей и наиболее рациональным распределением заказов и программ между предприятиями с учетом транспортных и эксплуатационных расходов. Отраслевое перспективное планирование использует главным образом полудинамические модели, с помощью которых решается задача достижения наилучшего результата развития отрасли к некоторому определенному моменту (например, каким образом на конец пятилетки можно получить заданный объем продукции с минимальными приведенными затратами, учитывающими капиталовложения и себестоимость). В гораздо меньшей степени отраслевое планирование использует пока собственно динамические модели, отражающие непрерывное развитие отрасли в течение всего планируемого периода. Это связано и со значительными сложностями, которые возникают при расчете таких моделей, и с трудностями получения необходимой информации на промежуточные годы. [c.210]
В моделях равновесного роста все или некоторые участники формируют свой спрос и предложение, решая динамическую задачу оптимизации. Для потребителя типичная задача состоит в максимизации суммы дисконтированных полезностей потребления за весь рассматриваемый период при совокупном бюджетном ограничении (сумма расходов на потребление в равновесных ценах не превосходит суммы доходов). Фирмы принимают решения о выпуске продукции и наращивании производственных мощностей на каждый момент рассматриваемого периода, максимизируя сумму прибыли за весь период. Равновесные цены в каждый момент времени балансируют спрос и предложение на потребительские блага и товары производственного назначения. Полтерови-чем в 1976 г. и Бьюли (Т. Bewley) в 1982 г. (см. ссылки в [10]) для двух различных вариантов таких моделей построена асимптотическая теория, аналогичная теории оптимального роста. В частности, для равновесных траекторий доказаны так называемые теоремы о магистрали, утверждающие, что если технологии и функции полезности меняются не слишком быстро, то с течением времени равновесные межотраслевые пропорции и соотношения цен перестают зависеть от начального состояния. Благодаря этому оказывается принципиально возможным исследовать характеристики долгосрочного развития на основе статических моделей равновесия типа Эрроу—Дебре. [c.497]
Приведенные выше формулы относятся к статической модели с минимизацией затрат за период. Однако доказано, что они верны и для бесконечношаговой модели с дисконтированным накоплением затрат и переносом возникающего дефицита в очередной период — при умножении цены закупки с на множитель 1 — a. В динамических задачах с конечным числом шагов оптимальные уровни запасов будут находиться между решениями для статического и динамического случаев. Точнее, [c.163]
Для решения задачи выбора оптимальных проектных вариантов в этом случае предлагается следующая трехэтапная многопродуктовая статическая экономико-математическая модель. [c.159]
Итак, каждому этажу планирования присуща своя оптимальная модель. Следуя этому принципу, советские экономисты создали математические модели оптимизации оперативно-календарного планирования, матричные модели техпромфинплана предприятия (планирование на уровне предприятия), модели размещения производства и оптимального плана перевозок (отраслевые задачи), оптимальные модели экономического района (региональное, районное планирование). Особое место среди всех названных занимает модель статического межотраслевого баланса, позволяющая планировать межотраслевую структуру народного хозяйства страны1. [c.19]
В качестве типичного примера полной модели в профессиональной литературе принято рассматривать модель, предложенную Сили (Sealey), см. [13]. В ней при описании поведения финансовой фирмы (посредника) учитываются как возможные действия по управлению портфелем рисковых активов, там и факторы издержек, а также проводимая политика воздействия на депозитные ставки. Сравнительно-статический анализ, осуществляемый в рамках модели Сили, позволяет определить воздействие несклонности к риску финансовых посредников на принятие ими оптимальных решений. Существуют и другие достаточно известные полные модели, например, модель Бал-тенспергера (Baltensperger), см. [2]. [c.211]
С целью упрощения анализа модели ее удобно редуцировать, заменив У (-), У (-) и У (-) на соответствующие функции оптимального отклика, которые можно обозначить через Л/ ( ), RJ ( ) и RJ ( ). Эти функции показывают объем производства, который производителю выгодно выбрать при данной предыстории игры. Редуцированная модель будет статической игрой, в которой участники выбирают только цены р1жр2. [c.565]
economy-ru.info
30.1. СЕТЕВЫЕ МОДЕЛИ. Основные понятия сетевой модели
До появления сетевых методов планирование работ, проектов осуществлялось в небольшом объеме. Наиболее известным средством такого планирования был ленточный график Ганта, недостаток которого состоит в том, что он не позволяет установить зависимости между различными операциями.
Современное сетевое планирование начинается с разбиения программы работ на операции. Определяются оценки продолжительности операций, и строится сетевая модель (график). Построение сетевой модели позволяет проанализировать все операции и внести улучшения в структуру модели до начала ее реализации. Строится календарный график, определяющий начало и окончание каждой операции, а также взаимосвязи с другими операциями графика. Календарный график выявляет критические операции, которым надо уделять особое внимание, чтобы закончить все работы в директивный срок. Что касается некритических операций, то календарный план позволяет определить резервы времени, которые можно выгодно использовать при задержке выполнения работ или эффективном применении как трудовых, так и финансовых ресурсов.
Сетевая модель — графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа. Граф — схема, состоящая из заданных точек (вершин), соединенных системой линий. Отрезки, соединяющие вершины, называются ребрами (дугами) графа. Ориентированным называется такой граф, на котором стрелкой указаны направления всех его ребер (дуг), что позволяет определить, какая из двух его граничных вершин является начальной, а какая — конечной. Исследование таких сетей проводится методами теории графов.
Теория графов оперирует понятием пути, объединяющим последовательность взаимосвязанных ребер. Контур означает такой путь, у которого начальная вершина совпадает с конечной. Сетевой график — это ориентированный граф без контуров. В сетевом моделировании имеются два основных элемента — работа и событие.
Работа — это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.
Фиктивная работа — это связь между результатами работ (событиями), не требующая затрат времени и ресурсов.
Событие — это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ.
Путь — это любая непрерывная последовательность (цепь) работ и событий.
Критический путь — это путь, не имеющий резервов и включающий самые напряженные работы комплекса. Работы, расположенные на критическом пути, называют критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.
При построении сетевых моделей необходимо соблюдать следующие правила.
1. Сеть изображается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.
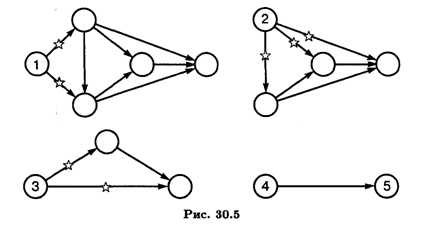
2. Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис. 30.1).
3. В сети не должно быть тупиков, т. е. промежуточных событий, из которых не выходит ни одна работа (рис. 30.2).
4. В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа (рис. 30.3).
5. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 30.4). Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. Из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычеркивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события. Пример нумерации сетевого графика показан на рис. 30.5.
Продолжительность выполнения работ устанавливается на основании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором — стохастическими (вероятностными).
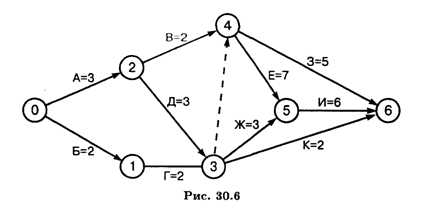
Рассмотрим в качестве примера программу создания нового бытового прибора, пользующегося спросом у населения. Необходимые данные приведены в табл. 30.1.
На основании данных таблицы построим сетевой график создания прибора с учетом вышеизложенных рекомендаций (рис. 30.6).
< Предыдущая Следующая >matica.org.ua
Статические и динамические информационные модели
Мы говорили об информационных моделях и об одном из видов программного обеспечения для работы с ними. Вы помните, что СУБД позволяет хранить большое количество информации и находить среди нее нужную. Однако, зачастую требуется не просто хранить некоторую информацию (знания об объектах), но и динамической39. Чаще всего правилами, описывающими функционирование системы являются математические формулы. В этом случае модель называют математической. Одним из средств для построения компьютерных математических моделей являются электронные таблицы (или табличные процессоры). Как ясно из названия, электронная таблица предназначена для табличных расчетов. Представление информации в ней похоже на реляционную базу данных. Но, в отличие от таблицы в базе данных, здесь строки совсем не обязательно должны быть однотипными (на рисунке 1-я и 151-я строки отличаются от остальных содержащих информацию строк).
Для того чтобы можно было записать правила, связывающие различные данные, все элементы таблицы имеют обозначения -- имена. Строки обозначаются числами, столбцы -- латинскими буквами. Если в таблице больше 26 столбцов, то после "Z" будет "AA", "AB" и т. д. Имя ячейки (клетки) таблицы образуется из имени столбца и номера строки, на пересечении которых она находится, например, "R37". Если же мы хотим указать, что действия выполняются с прямоугольной областью таблицы, нужно записать имена левой верхней и правой нижней клеток этой области, разделив их двумя точками (или, в зависимости от конкретной программы, двоеточием). Например, "F5..L27".
В каждую клетку таблицы можно занести число или текст (вспомните про типы данных!), а можно -- формулу. В этом случае компьютер выполнит заданные формулой действия, а на экране покажет результат.
Запись формул в компьютере несколько отличается от той, к которой вы привыкли. Например, в физике пишут "s=vt". Посмотрим, как такая формула будет выглядеть в электронной таблице? Пусть значение скорости находится в клетке B2, значение времени -- в клетке C2, а результат -- путь -- должен находиться в D2. В этом случае в ячейку D2 нужно вписать "=B2*C2". Какие же мы видим особенности записи?
Во-первых, формула начинается со знака "=", а обозначение искомой величины (в данном примере, пути) вообще отсутствует. Во-вторых, вместо переменных мы указываем имена ячеек таблицы, в которых содержатся их значения. В-третьих, используется специальный значок для обозначения умножения -- "*" (звездочка). Знаком деления является наклонная черта -- "/", для сложения и вычитания применяют обычные знаки -- "плюс" и "минус". Кроме того, формулы могут содержать функции. Причем не только математические (например, квадратный корень), но и функции, позволяющие упростить запись часто использующихся действий. К примеру, когда нужно найти общую стоимость полутора сотен товаров, то есть сложить значения ячеек, скажем, с D3 до D149, вместо длинной цепочки сложений достаточно написать "=SUM(D3..D149)". Существуют также функции (их называют условными), позволяющие выбирать те или иные действия в зависимости от значений каких-либо величин.
Обычно в электронной таблице одинаковые действия нужно выполнять с большим числом (нередко, с сотнями) строк таблицы. Неужели приходится по многу раз набирать почти одинаковые формулы? Конечно нет. В табличных процессорах предусмотрено автоматическое заполнение ячеек.
Поскольку чаще всего формула связывает между собой данные одной и той же строки (или одного и того же столбца) таблицы, при заполнении все входящие в формулу имена изменяются одновременно. Если в клетке D5 была формула "=B5*C5", то в клетку D6 будет вписано "=B6*C6", в D7 -- "=B7*C7" и так далее. Компьютер ориентируется на расположение клеток друг относительно друга. Такая адресация называется относительной. Но бывает нужна и абсолютная адресация -- когда значение какой-либо величины для всех формул находится в одной ячейке, и следовательно, ее имя при заполнении меняться не должно. В большинстве электронных таблиц, чтобы "закрепить" имя столбца или номер строки, перед ним ставится знак "$", например, "A$4", "$N87", "$W$52".
Но вот мы создали математическую модель, занесли данные в таблицу, выполнили расчеты -- и получили большое количество чисел. Хорошо бы представить результаты вычислений понагляднее. Тут нам тоже поможет табличный процессор. Оказывается, он умеет строить диаграммы.
Диаграмма40 -- условное графическое изображение числовых величин или их соотношений. Рассмотрим три их разновидности: столбчатую, линейную и круговую диаграммы.
Табличные процессоры позволяют строить не только несколько разновидностей диаграмм, но и графики (график, в отличие от диаграммы, изображает зависимость одной величины от другой).
Примечания
Statike (греч.) -- равновесие, неподвижность; dynamikos (греч.) -- сильный, действующий, движущийся.
Diagramma (греч.) -- рисунок.
mirznanii.com
- Dir 620 s c1

- Копировать подпись nt acronis что это

- Что такое path

- Что такое песочница в 360 total security

- Премиум для 360 total security
- Почистить ноутбук от ненужного хлама
- Как восстановить удаленную информацию из корзины компьютера

- Инструкция gimp 2 на русском языке

- Что такое система компьютерная

- Visual basic программа

- Локальная сеть в которой все компьютеры выполняют одинаковые функции называется

