ГлавнаяРазноеФункция fv в excel

Точность функции "FV" в Excel. Функция fv в excel


excel - Точность функции "FV" в Excel

Вот сценарий:

Инвестирование 10 фунтов стерлингов в месяц в течение 12 месяцев (инвестиции в начале месяца). Годовая эквивалентная норма прибыли 5%. Ежемесячно = 5%/12 = 0,4166667%

Теперь, используя функцию FV, это то, что я набрал:

=FV(0.00416666666666667,12,-10,0,1)

Ответ: £ 123,30

Теперь есть несколько способов сделать это вручную, о котором я могу думать (все похожие, но они получают одинаковый результат).

Это один из них:

A B c Monthly start amount¦Monthly interest rate¦ Respective rows of A*B 10 ¦ 0.004166667 ¦ 0.041666667 20 ¦ 0.004166667 ¦ 0.083333333 30 ¦ 0.004166667 ¦ 0.125 40 ¦ 0.004166667 ¦ 0.166666667 50 ¦ 0.004166667 ¦ 0.208333333 60 ¦ 0.004166667 ¦ 0.25 70 ¦ 0.004166667 ¦ 0.291666667 80 ¦ 0.004166667 ¦ 0.333333333 90 ¦ 0.004166667 ¦ 0.375 100 ¦ 0.004166667 ¦ 0.416666667 110 ¦ 0.004166667 ¦ 0.458333333 120 ¦ 0.004166667 ¦ 0.5 Then add up all of column C + the last figure on column A (120) = 120 + 3.25 = £123.25

Это, конечно, отличается от расчета FV. На самом деле это не так важно, но если вы инвестируете гораздо больше с более высокой процентной ставкой, то различия начинают становиться заметными.

Теперь мой вопрос: какой из них правильный, если его формула FV, тогда где я ошибаюсь в расчете на руководство?

спасибо

задан Boswell 13 авг. '14 в 17:35 источник поделиться

qaru.site

FV - Финансовые функции - Функции VBA - Справочники

Функция FV

FV(Rate, NPer, Pmt[, PV[, Due]])

Функция FV используется для вычисления конечного результата платежей для моделеи регулярных накоплений\выплат.Функция подходит для расчета выплат по закладной (например за дом) или итогов накоплений при ежемесячных банковских взносах

Возвращаемое значение

Возвращает значение типа Double, указывающее будущее значение суммы регулярных платежей при заданной учетной ставке

Параметры Функция содержит именованные аргументы
RateОбязательный аргумент типа Double, указывающее учетную ставку за период. Например, при выплате займа на приобретение автомобиля из расчета 10 процентов годовых, ежемесячная ставка составит 0 1/12, т.е. 0,0083
NPerОбязательный аргумент типа Integer, указывающее полное число периодов (выплат) за рассматриваемый срок. Например, если заем на приобретение автомобиля взят на четыре года, число месячных периодов (количество выплат) составит 4 * 12 (48)
PmtОбязательный аргумент типа Double, указывающее размер выплат за период. Каждый платеж включает как собственно возвращаемую сумму, так и проценты, которые не изменяются от одного платежа к другому
PVНеобязательный аргумент - выражение типа Variant, указывающее величину суммы на текущий момент. Например, при займе на покупку автомобиля, сумма займа является текущим значением при расчете будущих платежей. Если этот аргумент опущен, подразумевается значение 0
DueНеобязательный аргумент - Выражение типа Variant, указывающее режим выплат. Значение 0 означает, что платежи вносятся в конце каждого периода, а значение 1, что они вносятся в начале каждого периода. Если этот аргумент опущен, подразумевается значение 0
Примечание

Аргументы Rate и NPer должны задаваться в расчете на одну и ту же единицу времени. Например, если ставка Rate исчисляется за месяц, то и число периодов(выплат) NPer также следует указать в месяцах.Для всех аргументов выплаченные суммы (депозитные вклады и т.п.) представляются отрицательными значениями; а полученные (дивиденды) положительными

Пример ' В данном примере функция FV ' используется для вычисления суммы накоплений. ' В качестве исходных значений при расчете ' используется процентная ставка, ' возрастающая за определенный период (APR / 12), ' число выплат (TotPmts), размер платежа (Payment), ' текущий объем накоплений (PVal), а также ' режим выплат (PayType),т.е. число, определяющее, ' производятся платежи в начале или в конце периода. ' Так как Payment определяет выплачиваемые суммы, ' этой величине присваивается знак "минус" Dim Fmt, Payment, APR, TotPmts, PayType, PVal, FVal Const ENDPERIOD = 0, BEGINPERIOD = 1 ' Режим выплат Fmt = "###,###,##0.00" ' Денежный формат Payment = InputBox("Сколько предполагается вносить в месяц?") APR = InputBox("Какова ожидаемая годовая учетная ставка?") If APR > 1 Then APR = APR / 100 ' Правильная форма TotPmts = InputBox("Сколько месяцев вы будете вносить платежи?") PayType = MsgBox("Платежи вносятся в конце месяца?", vbYesNo) If PayType = vbNo Then PayType = BEGINPERIOD Else PayType = ENDPERIOD PVal = InputBox("Сколько денег имеется на счету сейчас?") FVal = FV(APR / 12, TotPmts, -Payment, -PVal, PayType) MsgBox "Будущий объем накоплений: " & Format(FVal, Fmt) & "." КатегорияФинансовые функции

www.excelworld.ru

Финансовые функции в Excel - Microsoft Excel для начинающих

Для иллюстрации наиболее популярных финансовых функций Excel, мы рассмотрим заём с ежемесячными платежами, процентной ставкой 6% в год, срок этого займа составляет 6 лет, текущая стоимость (Pv) равна $150000 (сумма займа) и будущая стоимость (Fv) будет равна $0 (это та сумма, которую мы надеемся получить после всех выплат). Мы платим ежемесячно, поэтому в столбце Rate вычислим месячную ставку 6%/12=0,5%, а в столбце Nper рассчитаем общее количество платёжных периодов 20*12=240.

Если по тому же займу платежи будут совершаться 1 раз в год, то в столбце Rate нужно использовать значение 6%, а в столбце Nper — значение 20.

ПЛТ

Выделяем ячейку A2 и вставляем функцию ПЛТ (PMT).

Пояснение: Последние два аргумента функции ПЛТ (PMT) не обязательны. Значение Fv для займов может быть опущено (будущая стоимость займа подразумевается равной $0, однако в данном примере значение Fv использовано для ясности). Если аргумент Type не указан, то считается, что платежи совершаются в конце периода.

Результат: Ежемесячный платёж равен $1074.65.

Совет: Работая с финансовыми функциями в Excel, всегда задавайте себе вопрос: я выплачиваю (отрицательное значение платежа) или мне выплачивают (положительное значение платежа)? Мы получаем взаймы сумму $150000 (положительное, мы берём эту сумму) и мы совершаем ежемесячные платежи в размере $1074.65 (отрицательное, мы отдаём эту сумму).

СТАВКА

Если неизвестная величина – ставка по займу (Rate), то рассчитать её можно при помощи функции СТАВКА (RATE).

КПЕР

Функция КПЕР (NPER) похожа на предыдущие, помогает рассчитать количество периодов для выплат. Если мы ежемесячно совершаем платежи в размере $1074.65 по займу, срок которого составляет 20 лет с процентной ставкой 6% в год, то нам потребуется 240 месяцев, чтобы выплатить этот заём полностью.

Это нам известно и без формул, но мы можем изменить ежемесячный платёж и увидеть, как это отразится на количестве платёжных периодов.

Вывод: Если мы будем ежемесячно вносить платёж в размере $2074.65 , то выплатим заём менее чем за 90 месяцев.

ПС

Функция ПС (PV) рассчитывает текущую стоимость займа. Если мы хотим выплачивать ежемесячно $1074.65 по взятому на 20 лет займу с годовой ставкой 6%, то какой размер займа должен быть? Ответ Вы уже знаете.

БС

В завершение рассмотрим функцию БС (FV) для расчёта будущей стоимости. Если мы выплачиваем ежемесячно $1074.65 по взятому на 20 лет займу с годовой ставкой 6%, будет ли заём выплачен полностью? Да!

Но если мы снизим ежемесячный платёж до $1000, то по прошествии 20 лет мы всё ещё будем в долгах.

Оцените качество статьи. Нам важно ваше мнение:

office-guru.ru

Функция FV - Access

Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).

Возвращает значение типа Double, указывающее будущее значение ежегодного платежа на основе периодических постоянных выплат и постоянной процентной ставки.

Синтаксис

Бс ( ставка, кпер ПЛТ [, Пс ] [Тип ] )

Синтаксис функции бс имеет следующие аргументы:

Аргумент

Описание

ставка

Обязательный аргумент. Значение double, обозначающее процентную ставку за период. Например, если вы берете кредит на автомобиль с годовой процентной ставкой, равной 10 %, и ежемесячными выплатами, ставка за период будет равна 0,1/12 (0,0083).

кпер

Обязательный аргумент. Целое число, указывающее общее количество периодов оплаты. Например, при ежемесячных выплатах по четырехгодичному кредиту на машину число периодов выплат равно 4*12 (или 48).

плт

Обязательный аргумент. Значение double, обозначающее платеж, который должен выплачиваться в каждый период. Обычно платежи включают основную сумму и проценты, которые не изменяются на протяжении всего периода выплат.

пс

Необязательно:. Значение типа Variant, указывающее текущее значение (или общей суммы) из ряда будущих выплат. Например взят купить автомобиль, сумма займа является приведенную стоимость предстоящих ежемесячных платежей за автомобиль, которые нужно сделать. Если не указано, предполагается, что 0.

тип

Необязательный аргумент. Вариант, определяющий, когда должна производиться выплата. Укажите значение 0, если платежи выплачиваются в конце периода оплаты, или 1, если они выплачиваются в начале периода. Если этот аргумент не задан, используется значение 0.

Замечания

Выплатами называется ряд фиксированных платежей наличными, которые выполняются в определенный период времени. Это может быть заём (например, ипотека) или инвестиция (например, сберегательный вклад с ежемесячным пополнением).

При вычислении значений ставка и кпер нужно использовать периоды оплаты, выраженные в одних и тех же единицах. Например, если ставка вычисляется с использованием месяцев, значение кпер также должно рассчитываться с использованием месяцев.

Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются отрицательными числами, а получаемые (например, дивиденды) — положительными.

Пример

Примечание: В примерах ниже показано, как использовать эту функцию в модуле Visual Basic для приложений (VBA). Чтобы получить дополнительные сведения о работе с VBA, выберите Справочник разработчика в раскрывающемся списке рядом с полем Поиск и введите одно или несколько слов в поле поиска.

В этом примере используется функция бс Возвращает будущую стоимость инвестиции процентную ставку, начисляемые за период общее количество платежей (TotPmts) платежа (Payment) текущее значение (APR / 12) инвестиции (PVal) и число, которое указывает, является ли платеж в начале или в конце периода оплаты (PayType). Обратите внимание, что из-за Payment представляет выплачиваемую, отрицательное число.

Dim Fmt, Payment, APR, TotPmts, PayType, PVal, FValConst ENDPERIOD = 0, BEGINPERIOD = 1 ' When payments are made.Fmt = "###,###,##0.00" ' Define money format.Payment = InputBox("How much do you plan to save each month?")APR = InputBox("Enter the expected interest annual percentage rate.")If APR > 1 Then APR = APR / 100 ' Ensure proper form.TotPmts = InputBox("For how many months do you expect to save?")PayType = MsgBox("Do you make payments at the end of month?", vbYesNo)If PayType = vbNo Then PayType = BEGINPERIOD Else PayType = ENDPERIODPVal = InputBox("How much is in this savings account now?")FVal = FV(APR / 12, TotPmts, -Payment, -PVal, PayType)MsgBox "Your savings will be worth " & Format(FVal, Fmt) & "."

support.office.com

Функция БС - Служба поддержки Office

Примечание:  Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке) .

БС — одна из финансовых функций, возвращающая будущую стоимость инвестиции на основе постоянной процентной ставки. В функции БС можно использовать как периодические постоянные платежи, так и единый общий платеж.

Используйте Excel Formula Coach для расчета будущей стоимости платежей. Одновременно вы узнаете, как использовать функции бс в формуле.

Или с помощью Excel Formula Coach найти будущее значение типа single, общая сумма платежа.

Синтаксис

БС(ставка;кпер;плт;[пс];[тип])

Дополнительные сведения об аргументах функции БС и других функциях, связанных с аннуитетами, см. в описании функции ПС.

Аргументы функции БС описаны ниже.

  • Ставка    — обязательный аргумент. Процентная ставка за период.

  • Кпер    — обязательный аргумент. Общее количество периодов платежей по аннуитету.

  • Плт     — обязательный аргумент. Выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно аргумент "плт" состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент "пс" является обязательным.

  • Пс     — обязательный аргумент. Приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент "пс" опущен, предполагается значение 0. В этом случае аргумент "плт" является обязательным.

  • Тип     — необязательный аргумент. Число 0 или 1, обозначающее срок выплаты. Если аргумент "тип" опущен, предполагается значение 0.

Тип

Выплата

0

В конце периода

1

В начале периода

Замечания

  • Убедитесь, что единицы измерения аргументов "ставка" и "кпер" используются согласованно. При ежемесячных выплатах по четырехгодичному займу из расчета 12 процентов годовых используйте значение 12%/12 в качестве аргумента "ставка" и 4*12 — в качестве аргумента "кпер". При ежегодных платежах по тому же займу используйте значение 12% в качестве аргумента "ставка" и 4 — в качестве аргумента "кпер".

  • Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются отрицательными числами, а получаемые (например, дивиденды) — положительными.

Примеры

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные

Описание

0,06

Годовая процентная ставка

10

Количество платежей

-200

Объем платежей

-500

Стоимость на текущий момент

1

Платежи осуществляются в начале периода (0 означает, что платежи осуществляются в конце периода)

Формула

Описание

Результат

=БС(A2/12; A3; A4; A5; A6)

Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A5.

2 581,40 ₽

Пример 2

Данные

Описание

0,12

Годовая процентная ставка

12

Количество платежей

-1000

Объем платежей

Формула

Описание

Результат

=БС(A2/12; A3; A4)

Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A4.

12 682,50 ₽

Пример 3

Данные

Описание

0,11

Годовая процентная ставка

35

Количество платежей

-2000

Объем платежей

1

Платежи осуществляются в начале года (0 означает конец года)

Формула

Описание

Результат

=БС(A2/12; A3; A4;; A5)

Будущая стоимость инвестиций с условиями, указанными в ячейках A2:A4.

82 846,25 ₽

Пример 4

Данные

Описание

0,06

Годовая процентная ставка

12

Количество платежей

-100

Объем платежей

-1000

Стоимость на текущий момент

1

Платежи осуществляются в начале года (0 означает конец года)

Формула

Описание

Результат

=БС(A2/12; A3; A4; A5; A6)

Будущая стоимость инвестиций при условиях, указанных в ячейках A2:A5.

2 301,40 ₽

support.office.com

Инвестиции и аннуитет в Excel

Этот пример покажет вам, как рассчитать будущую стоимость инвестиций и текущую стоимость аннуитета.

Совет: При работе с финансовыми функциями Excel всегда задавайте себе вопрос, я оплачиваю (расход) или я получаю деньги (доход)?

Инвестиции

Предположим, что в конце каждого года, вы кладёте $100 на сберегательный счет. Какую сумму вы получите через 10 лет с годовой процентной ставкой 8%?

  1. Вставьте функцию FV (Future Value), в русском варианте – БС (Будущая Стоимость).

    =FV(rate,nper,pmt,[pv],[type])=БС(ставка;кпер;плт;[пс];[тип])

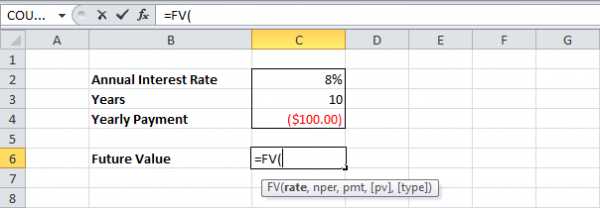
  2. Введите аргументы:

    =FV(C2,C3,C4)=БС(C2;C3;C4)

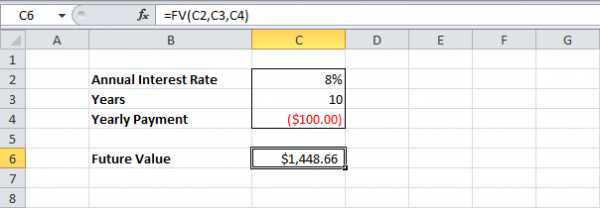
    За 10 лет вы положите на депозит 10*100 = $1000 (расход). А по истечении срока получите $1448,66 (доход). Чем больше сумма, тем быстрее приумножаются ваши деньги.

Примечание: Последние два аргумента необязательны. Если опустить аргумент pv (пс), он будет равен 0 (нет текущей стоимости). Если опустить аргумент type (тип), то предполагается, что платежи должны поступать в конце периода.

Аннуитет

Предположим, вы хотите купить аннуитет, который будет приносить $600 в месяц в течение следующих 20 лет. Сколько будет стоить аннуитет с годовой процентной ставкой 6%?

  1. Вставьте функцию PV (Present Value), в русском варианте – ПС (Приведенная Стоимость).

    =PV(rate,nper,pmt,[fv],[type])=ПС(ставка;кпер;плт;[бс];[тип])

  2. Введите аргументы:

    =PV(C4/12,C5*12,C6)=ПС(C4/12;C5*12;C6)

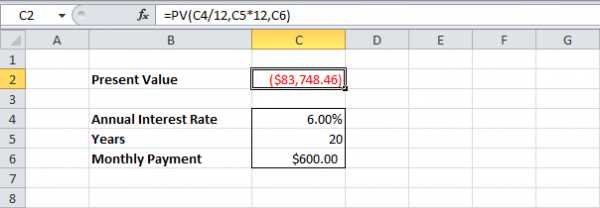
    Вам нужно внести одноразовый платеж в размере $83748,46 (расход), чтобы оплатить этот аннуитет. В будущем вы будете получать 240*600 (доход) = $144000. Это еще один пример того, что деньги растут с течением времени.

Примечание: Мы получаем ежемесячные платежи, поэтому используем формулу 6/12 = 0,5% для тарифа и 20*12 = 240 для аргумента nper (кпер). Последние два аргумента необязательны. Если опущен аргумент fv (бс), значит, он равен 0 (нет будущего значения). Если опущен аргумент type (тип), то предполагается, что платежи должны поступить в конце периода. Этот аннуитет не принимает во внимание продолжительность жизни, инфляцию и т.д.

Оцените качество статьи. Нам важно ваше мнение:

office-guru.ru

Как при помощи Excel считать величину дисконтированного (приведенного) денежного потока — Трюки и приемы в Microsoft Excel

К наиболее типичным методам финансового анализа можно отнести анализ затрат, период окупаемости инвестиций, денежный поток и внутрифирменный коэффициент окупаемости инвестиций. Каждый из этих методов мы рассмотрим далее.

Анализ затрат

Анализ затрат является довольно простым методом. В этом случае вы определяете стоимость производства продукта (которым в нашем случае является проект) и сопоставляете ее с ожидаемыми выгодами. Если выгоды перекрывают затраты, то, скорее всего, данный проект будет принят к исполнению.

При выполнении этого анализа не забывайте включить все затраты. Обычно сюда входит совокупная стоимость таких процессов, как практическая реализация проекта, текущая поддержка, сопровождение (техобслуживание), содержание соответствующего персонала, устранение проблем, которые не удалось решить в ходе выполнения проекта, и т.д. В этой методике полная стоимость проекта рассчитывается не по факту выполненных работ, а на основании результатов, полученных в итоге выполнения этого проекта, и только после того, как они будут внедрены в данной организации.

Период окупаемости инвестиций

Период окупаемости инвестиций — это количество времени, которое требуется для того, чтобы окупились первоначальные инвестиции в данный проект. Совокупная стоимость проекта сравнивается с получаемыми доходами и вычисляется время, которое требуется для того, чтобы полученные доходы превысили затраты на реализацию данного проекта. Когда выполняется сравнение двух или большего числа проектов сходного масштаба и сложности, как правило, выбирается проект с наименьшим периодом окупаемости инвестиций. У этого метода нет «универсальной» формулы, которая позволяла бы быстро найти требуемое решение. Если, например, себестоимость проекта равняется 100 000 долл., а ожидаемые доходы составляют 25 000 долл. в квартал, то период окупаемости инвестиций составит один год.

Дисконтированные (приведенные) денежные потоки

Если вам предложат 1 000 долл. сегодня или те же 1 000 долл. через два года, какой вариант вы предпочтете? Ответ предсказуем, поскольку вложив сейчас эту сумму в банк или какое-либо предприятие, через два года вы будете иметь с нее прибыль. Например, под 6% годовых такая инвестиция на двухлетний период составит 1 123,60 долл. (в нынешних долларах, разумеется).

Метод дисконтированного (приведенного) денежного потока сравнивает стоимость будущих денежных потоков с нынешними долларами. Иными словами, он выполняет операцию, противоположную той, которую мы только что объяснили. Зная, что ваш проект принесет через два года сумму, равную 1 123,60 долл. (это так называемая будущая стоимость — Future Value, или FV), вы бы смогли с помощью метода дисконтированного (приведенного) денежного потока определить нынешнюю стоимость этой суммы. Ответ, конечно же, таков: 1 000 долл.

Чтобы иметь представление о дисконтированных денежных потоках, вы должны знать стоимость соответствующих инвестиций в нынешних долларах, иначе говоря, приведенную стоимостью (Present Value, или PV), которая вычисляется следующим образом: PV=FV/(1+i)n. Эта формула говорит о том, что приведенная стоимость равняется будущей стоимости инвестиций, деленной на один, плюс процентная ставка, возведенная в степень, равную количеству периодов, на которые мы инвестируем нашу сумму.

Вам не нравится математика? Но это же так просто! В Excel предусмотрена встроенная функция для вычисления приведенной стоимости (наряду со множеством других функций, позволяющих выполнять финансовые расчеты). На рисунке ниже показана группа Function Library (Библиотека функций), предусмотренная на вкладке Formulas (Формулы), и часть списка финансовых функций, встроенных в Excel.

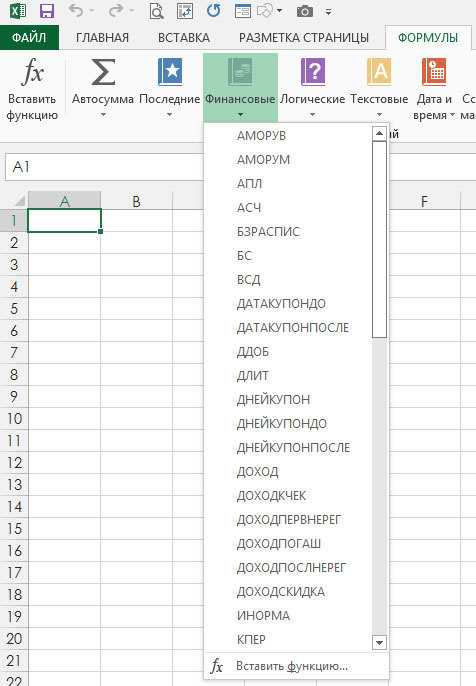
Рис. 1. Финансовые функции, представленные в библиотеке функций и перечень финансовых функций

Вернемся, однако, к нашей формуле для вычисления приведенной стоимости инвестиций. Выберите в списке функций элемент PV (в русифицированной версии Excel — ПС (Приведенная стоимость)). На экране появится диалоговое окно Function Arguments (Аргументы функции), показанное на рис. 2.

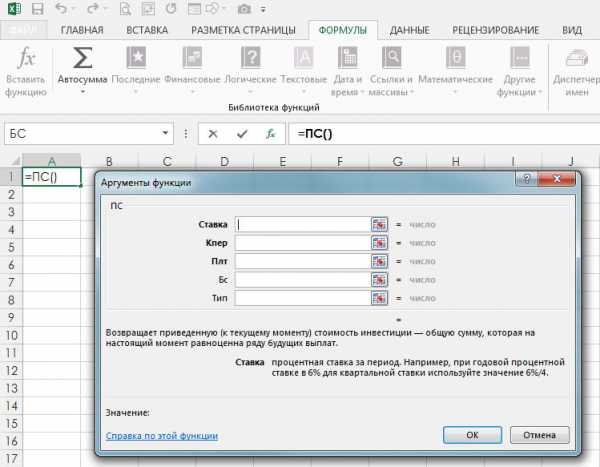
Рис. 2. Диалоговое окно Function Arguments для функции PV

Диалоговое окно Function Arguments предназначено для ввода значений отдельных элементов выбранной вами функции, которые необходимы для вычисления приведенной стоимости. В текстовом поле Rate (Ставка) этого диалогового окна следует ввести величину процентной ставки за определенный временной период. Вы можете ввести 6% или 0,06 (предполагается, что процент начисляется ежегодно по методу сложных процентов). Если бы процент начислялся ежеквартально (по тому же методу), тогда вам нужно было бы разделить указанную величину процентной ставки на 4, а затем ввести полученный результат в поле Rate (Ставка).

Ниже находится поле Nper (Кпер), в котором вводят количество временных периодов. Мы инвестируем нашу сумму на два года. Величина выплаты (поле Pmt (Плт)) равняется 0, поскольку мы не производим выплат по этой инвестиции, а просто хотим знать величину всей этой суммы в нынешних долларах. Далее находится поле FV (Бс), в котором вводят значение будущей стоимости. В нашем примере будущая стоимость инвестиции равняется -1 123,60 долл. Если в поле FV (Бс) ввести положительное число, то результат вычисления этой функции будет отрицательным. На рис. 3. показано диалоговое окно Function Arguments со значениями аргументов функции PV (Приведенная стоимость), введенных в соответствующие поля.

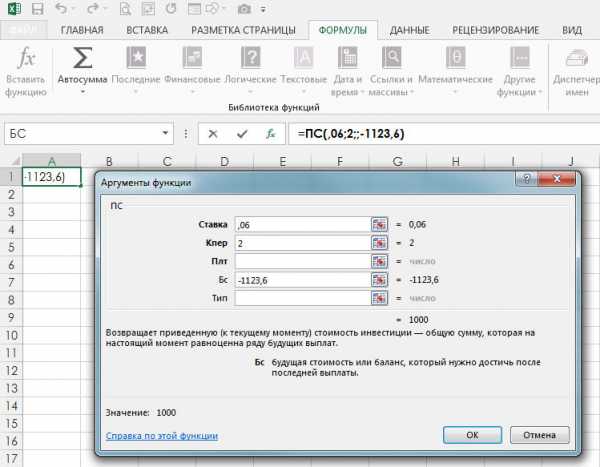
Рис. 3. Аргументы функции PV

Вместо числовых значений в полях диалогового окна Function Arguments (Аргументы функции) можно дать адрес ячейки, в которой введено нужное вам значение. Предположим, например, что в ячейке С1 введено число 0,06. В этом случае в текстовом поле Rate (Процентная ставка) диалогового окна Function Arguments достаточно указать только адрес упомянутой выше ячейки, т.е. С1. Непосредственно под текстовыми полями диалогового окна Function Arguments представлен результат наших вычислений функции PV (Приведенная стоимость). В нашем случае PV=1000. Помимо диалогового окна Function Arguments аргументы данной функции отображены в строке формул программы Excel, а также в активизированной ячейке (А1 в данном случае) (см. рис. 3.).

Как видите, сначала следует значение процентной ставки, затем количество периодов и будущая стоимость. Обратите внимание, что в данной функции отсутствует значение между двумя запятыми. Это означает, что один из аргументов функции равен нулю (в нашем случае величина выплаты (поле Pmt (Плт)). (В русифицированной версии программы Excel аргументы функций следует отделять друг от друга точкой с запятой (;)) Как только выщелкнете на кнопке ОК, в ячейке А1 появится результат вычисления функции, в нашем случае — 1 000 долл.

Для того чтобы воспользоваться функцией PV (ПС), не обязательно перебирать ряд интерфейсных элементов программы. Для этого достаточно просто ввести =pv() в ячейке А1. В результате ваших действий на экране появится экранная подсказка, в которой приведен синтаксис данной функции, т.е. сокращенные названия и очередность ее аргументов (рис. 4).

Рис. 4. Всплывающая подсказка с перечнем аргументов функции PV

Если вы не знаете точно, какие значения следует вводить в качестве аргументов функции, откройте окно справочной системы Excel. В единственном текстовом поле этого окна введите PV (ПС для русифицированной Excel) и нажмите клавишу Enter. Справочная система немедленно отобразит всю необходимую информацию по интересующей вас функции.

Если вы, как и большинство других пользователей, раздражаетесь из-за того, что окно справочной системы Excel время от времени скрывается за вашей электронной таблицей (когда вы пытаетесь выполнять пошаговые инструкции, приведенные в этом окне), выполните следующее: скопируйте, а затем вставьте информацию, представленную в окне справки, в электронную таблицу, а затем, когда вы введете нужные значения в формулу, удалите эту информацию.

Допустим, что ваш комитет по отбору проектов рассматривает три проекта, из которых необходимо выбрать самый подходящий. Ожидается, что проект А принесет через два года 130 000 долл. прибыли; проект В — 140 000 долл. через три года; а проект С — 148 000 долл. через четыре года. Какому из этих проектов должен отдать предпочтение комитет, если свое решение он основывает лишь на использовании метода дисконтированного (приведенного) денежного потока, полагая, что процентная ставка равняется 8%? Самую высокую прибыль обеспечивает проект А. На рис. 5 показаны расчетные формулы по каждому проекту и полученные с их помощью результаты.

Рис. 5. Сравнение проектов с помощью метода дисконтированного (приведенного) денежного потока

excelexpert.ru